viernes, 30 de junio de 2017
miércoles, 28 de junio de 2017
Aplicación del teorema de la probabilidad total y del teorema de Bayes
ENUNCIADO. eL $40\,\%$ de los sábados Marta va al cine, el $30\,\%$ va de compras y el $30\,\%$ restante juega a videojuegos. Cuando va al cine, el $60\,\%$ de las veces lo hace con sus compañeros de baloncesto. Lo mismo ocurre el $20\,\%$ de las veces que va de compras, y el $80\,\%$ de las veces que juega a videojuegos. Se pide:
a) Hallar la probabilidad de que el próximo sábado Marta no quede con sus compañeros de baloncesto
b) Si se sabe que Marta ha quedado con sus compañeros de baloncesto, ¿ cuál es la probabilidad de que vayan al cine ?
SOLUCIÓN.
a)
Denotemos por: $C$ el suceso 'ir al cine'; $R$, 'ir de compras'; $V$, 'jugar a videojuegos'; y $B$, 'ir con los compañeros de baloncesto'. Según el enunciado, $P(C)=\dfrac{40}{100}=\dfrac{2}{5}$, $P(R)=\dfrac{30}{100}=\dfrac{3}{10}$, $P(V)=\dfrac{30}{100}=\dfrac{3}{10}$; $P(B|C)=\dfrac{60}{100}=\dfrac{3}{5} $; $P(B|R)=\dfrac{20}{100}=\dfrac{1}{5}$ y $P(B|V)=\dfrac{80}{100}=\dfrac{4}{5}$
Entonces, $B=(B\cap C) \cup (B\cap R) \cup (B\cap V)$ y como $(B\cap C) \cap (B\cap R) \cap (B\cap V) = \emptyset$ ( son incompatibles ), podemos escribir $P(B)=P(B\cap C)+P(B\cap R)+P(B\cap V)$ que, por la definición de probabilidad condicionada, puede ponerse de la forma ( teorema de la probabilidad total ) $$P(B)=P(B|C)P(C)+P(B|R)P(R)+P(B|V)P(V)$$ y con los datos obtenemos $$P(B)=\dfrac{3}{5}\cdot \dfrac{2}{5}+\dfrac{1}{5}\cdot \dfrac{3}{2}+\dfrac{4}{5}\cdot \dfrac{3}{10}=\dfrac{27}{50}$$ luego la probabilidad pedida de $\bar{B}$ ( 'no quedar con los compañeros de baloncesto' ) es igual a $$P(\bar{B})=1-P(B)=1-\dfrac{27}{50}=\dfrac{23}{50}$$
b)
$$P(C|B)\overset{\text{teorema de Bayes}}{=}\dfrac{P(B|C)P(C)}{P(B)}=\dfrac{\dfrac{3}{5}\cdot \dfrac{2}{5}}{\dfrac{27}{50}}=\dfrac{4}{9}$$
$\square$
a) Hallar la probabilidad de que el próximo sábado Marta no quede con sus compañeros de baloncesto
b) Si se sabe que Marta ha quedado con sus compañeros de baloncesto, ¿ cuál es la probabilidad de que vayan al cine ?
SOLUCIÓN.
a)
Denotemos por: $C$ el suceso 'ir al cine'; $R$, 'ir de compras'; $V$, 'jugar a videojuegos'; y $B$, 'ir con los compañeros de baloncesto'. Según el enunciado, $P(C)=\dfrac{40}{100}=\dfrac{2}{5}$, $P(R)=\dfrac{30}{100}=\dfrac{3}{10}$, $P(V)=\dfrac{30}{100}=\dfrac{3}{10}$; $P(B|C)=\dfrac{60}{100}=\dfrac{3}{5} $; $P(B|R)=\dfrac{20}{100}=\dfrac{1}{5}$ y $P(B|V)=\dfrac{80}{100}=\dfrac{4}{5}$
Entonces, $B=(B\cap C) \cup (B\cap R) \cup (B\cap V)$ y como $(B\cap C) \cap (B\cap R) \cap (B\cap V) = \emptyset$ ( son incompatibles ), podemos escribir $P(B)=P(B\cap C)+P(B\cap R)+P(B\cap V)$ que, por la definición de probabilidad condicionada, puede ponerse de la forma ( teorema de la probabilidad total ) $$P(B)=P(B|C)P(C)+P(B|R)P(R)+P(B|V)P(V)$$ y con los datos obtenemos $$P(B)=\dfrac{3}{5}\cdot \dfrac{2}{5}+\dfrac{1}{5}\cdot \dfrac{3}{2}+\dfrac{4}{5}\cdot \dfrac{3}{10}=\dfrac{27}{50}$$ luego la probabilidad pedida de $\bar{B}$ ( 'no quedar con los compañeros de baloncesto' ) es igual a $$P(\bar{B})=1-P(B)=1-\dfrac{27}{50}=\dfrac{23}{50}$$
b)
$$P(C|B)\overset{\text{teorema de Bayes}}{=}\dfrac{P(B|C)P(C)}{P(B)}=\dfrac{\dfrac{3}{5}\cdot \dfrac{2}{5}}{\dfrac{27}{50}}=\dfrac{4}{9}$$
$\square$
Geometría analítica
ENUNCIADO.
a) Determinar la distancia entre las rectas $r_1:x=y=z$ y $r_2:\left\{\begin{matrix}x+y-1=0\\ x-z+1=0\end{matrix}\right.$
b) Obténgase el punto de corte de la recta $s:x=2-y=z-1$ con el plano perpendicular a $s$ que pasa por el origen de coordenadas
SOLUCIÓN.
a)
En primer lugar vamos a estudiar la incidencia entre $r_1$ y $r_2$.
Un vector director de $r_1$ es $\vec{u}_1=(1,1,1)$
Encontremos ahora un vector director de $r_2$. De las ecuaciones implícitas de la recta podemos escribir la misma en forma paramétrica de la forma $\left\{\begin{matrix}x&=&-\lambda+2 \\ y&=&\lambda-1 \\ z&=&\lambda \end{matrix}\right.$ y despejando el parámetro $\lambda$ de cada una de ellas, $\left\{\begin{matrix}\lambda&=&\dfrac{x-2}{-1}\\ \lambda&=&y+1 \\ \lambda&=&z \end{matrix}\right.$ por lo que la ecuación en forma continua es $\dfrac{x-2}{-1}=\dfrac{y-(-1)}{1}=\dfrac{z}{1}$ y de ello deducimos que un vector director de $r_2$ es $\vec{u}_2=(-1,1,1)$
A continuación necesitamos conocer un punto de cada una de las dos rectas, que denotaremos por $P_{r_1}$ y $P_{r_2}$ para construir un vector que apunte de uno a otro ( de una recta a la otra ): $\vec{P_{r_1}P_{r_2}}$, ya que: i) si $\text{rango}\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}=3$ las rectas se cruzan pero no se cortan, con lo cual la distancia pedida será distinta de cero, y, ii) en caso de que $\text{rango}\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}=2$ y $\text{rango}\{\vec{u}_1,\vec{u}_2\}=1$, las rectas son paralelas y distintas, con lo cual la distancia entre estas también es distinta de cero.
Es evidente que un punto de $r_1$ es $P_{r_1}=(0,0,0)$. Por otra parte, fijando el parámetro $\lambda$ ( pongamos que $\lambda:=0$ ) en las ecuaciones paramétricas de $r_2$, encontramos un punto de la misma, $P_{r_2}=(2,-1,0)$. Hecho esto, $\vec{P_{r_1}P_{r_2}}=(2-0,-1-0,0-0)=(2,-1,0)$
Como $\begin{vmatrix}1&1&1\\-1&1&1\\2&-1&0\end{vmatrix}=2\neq 0$, deducimos de ello que $\text{rango}\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}=3$ y por tanto $r_1$ y $r_2$ se cruzan pero no se cortan, con lo cual la distancia pedida es distinta de cero.
Para calcular la distancia $d(r_1,r_2)$, tendremos en cuenta que los vectores $\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}$ forman un paralelepípedo de volumen igual al valor absoluto del producto mixto de los tres $\left|[\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}]\right|$, pero ese mismo volumen puede calcularse también mediante $d(r_1,r_2)\cdot \left\|\vec{u}_1 \times \vec{u}_2\right\|$ luego $$d(r_1,r_2)=\dfrac{\left|[\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}]\right|}{\left\|\vec{u}_1 \times \vec{u}_2\right\|} \quad \quad (1)$$
donde
$$\left|[\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}]\right|=2$$ ya que $$\begin{vmatrix}1&1&1\\-1&1&1\\2&-1&0\end{vmatrix}=2$$
Por otra parte $$\vec{u}_1 \times \vec{u}_2=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\1&1&1\\-1&1&1\end{vmatrix}=2\,\vec{k}=(0,-2,2)$$ luego $\left\|\vec{u}_1 \times \vec{u}_2\right\|=2\,|\sqrt{2}|$. Y, finalmente, sustituyendo en (1) llegamos a $$d(r_1,r_2)=\dfrac{2}{2\,|\sqrt{2}|}=\dfrac{|\sqrt{2}|}{2}$$
b)
La recta $s$ puede expresarse de la forma ( continua ) $s:\dfrac{x}{1}=\dfrac{y-2}{-1}=\dfrac{z-1}{1} \quad \quad (2)$, luego un vector director de la recta es $\vec{u}_s=(1,-1,1)$, que a su vez es un vector perpendicular al plano $\pi$ ( perpendicular a $s$ ); entonces, como la ecuación general de un plano es $Ax+By+Cz+D=0$ y $A=1$, $B=-1$ y $C=1$, podemos escribir $\pi:x-y+z+D=0 \quad \quad (3) $. Y como sabemos que $O(0,0,0)$ es un punto de $\pi$, deducimos ( sustituyendo las coordenadas de $O$ en la ecuación (3) ) que $D=0$, con lo cual vemos que la ecuación del plano pedido es $$\pi:x-y+z=0$$
La ecuación de la recta (2) también podemos expresarla en forma implícita (como la intersección de dos planos): $$s:\left\{\begin{matrix}x=2-y\\x=z-1\end{matrix}\right.$$ que junto con la ecuación del plano $\pi:x-y+z=0$ nos lleva al sistema de ecuaciones $$\left\{\begin{matrix}x&-&y&+&z&=&0 \\ x&+&y&&&=&2 \\ x&&&-&z&=&-1\end{matrix}\right. \sim \left\{\begin{matrix}x&-&y&+&z&=&0 \\ &&2y&-&z&=&2 \\ &&y&-&2z&=&-1\end{matrix}\right.\sim$$
$$\sim \left\{\begin{matrix}x&-&y&+&z&=&0 \\ &&2y&-&z&=&2 \\ &&&&3z&=&4\end{matrix}\right.$$ con lo cual, despejando de la última ecuación, $z=\dfrac{4}{3}$; sustituyendo en la segunda, $y=\dfrac{5}{3}$; y, sustituyendo estos dos valores en la primera ecuación, $x=\dfrac{1}{3}$. Así pues el punto de corte viene dado por $( \dfrac{1}{3}\,,\,\dfrac{5}{3}\,,\,\dfrac{4}{3})$
$\square$
a) Determinar la distancia entre las rectas $r_1:x=y=z$ y $r_2:\left\{\begin{matrix}x+y-1=0\\ x-z+1=0\end{matrix}\right.$
b) Obténgase el punto de corte de la recta $s:x=2-y=z-1$ con el plano perpendicular a $s$ que pasa por el origen de coordenadas
SOLUCIÓN.
a)
En primer lugar vamos a estudiar la incidencia entre $r_1$ y $r_2$.
Un vector director de $r_1$ es $\vec{u}_1=(1,1,1)$
Encontremos ahora un vector director de $r_2$. De las ecuaciones implícitas de la recta podemos escribir la misma en forma paramétrica de la forma $\left\{\begin{matrix}x&=&-\lambda+2 \\ y&=&\lambda-1 \\ z&=&\lambda \end{matrix}\right.$ y despejando el parámetro $\lambda$ de cada una de ellas, $\left\{\begin{matrix}\lambda&=&\dfrac{x-2}{-1}\\ \lambda&=&y+1 \\ \lambda&=&z \end{matrix}\right.$ por lo que la ecuación en forma continua es $\dfrac{x-2}{-1}=\dfrac{y-(-1)}{1}=\dfrac{z}{1}$ y de ello deducimos que un vector director de $r_2$ es $\vec{u}_2=(-1,1,1)$
A continuación necesitamos conocer un punto de cada una de las dos rectas, que denotaremos por $P_{r_1}$ y $P_{r_2}$ para construir un vector que apunte de uno a otro ( de una recta a la otra ): $\vec{P_{r_1}P_{r_2}}$, ya que: i) si $\text{rango}\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}=3$ las rectas se cruzan pero no se cortan, con lo cual la distancia pedida será distinta de cero, y, ii) en caso de que $\text{rango}\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}=2$ y $\text{rango}\{\vec{u}_1,\vec{u}_2\}=1$, las rectas son paralelas y distintas, con lo cual la distancia entre estas también es distinta de cero.
Es evidente que un punto de $r_1$ es $P_{r_1}=(0,0,0)$. Por otra parte, fijando el parámetro $\lambda$ ( pongamos que $\lambda:=0$ ) en las ecuaciones paramétricas de $r_2$, encontramos un punto de la misma, $P_{r_2}=(2,-1,0)$. Hecho esto, $\vec{P_{r_1}P_{r_2}}=(2-0,-1-0,0-0)=(2,-1,0)$
Como $\begin{vmatrix}1&1&1\\-1&1&1\\2&-1&0\end{vmatrix}=2\neq 0$, deducimos de ello que $\text{rango}\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}=3$ y por tanto $r_1$ y $r_2$ se cruzan pero no se cortan, con lo cual la distancia pedida es distinta de cero.
Para calcular la distancia $d(r_1,r_2)$, tendremos en cuenta que los vectores $\{\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}\}$ forman un paralelepípedo de volumen igual al valor absoluto del producto mixto de los tres $\left|[\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}]\right|$, pero ese mismo volumen puede calcularse también mediante $d(r_1,r_2)\cdot \left\|\vec{u}_1 \times \vec{u}_2\right\|$ luego $$d(r_1,r_2)=\dfrac{\left|[\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}]\right|}{\left\|\vec{u}_1 \times \vec{u}_2\right\|} \quad \quad (1)$$
donde
$$\left|[\vec{u}_1,\vec{u}_2,\vec{P_{r_1}P_{r_2}}]\right|=2$$ ya que $$\begin{vmatrix}1&1&1\\-1&1&1\\2&-1&0\end{vmatrix}=2$$
Por otra parte $$\vec{u}_1 \times \vec{u}_2=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\1&1&1\\-1&1&1\end{vmatrix}=2\,\vec{k}=(0,-2,2)$$ luego $\left\|\vec{u}_1 \times \vec{u}_2\right\|=2\,|\sqrt{2}|$. Y, finalmente, sustituyendo en (1) llegamos a $$d(r_1,r_2)=\dfrac{2}{2\,|\sqrt{2}|}=\dfrac{|\sqrt{2}|}{2}$$
b)
La recta $s$ puede expresarse de la forma ( continua ) $s:\dfrac{x}{1}=\dfrac{y-2}{-1}=\dfrac{z-1}{1} \quad \quad (2)$, luego un vector director de la recta es $\vec{u}_s=(1,-1,1)$, que a su vez es un vector perpendicular al plano $\pi$ ( perpendicular a $s$ ); entonces, como la ecuación general de un plano es $Ax+By+Cz+D=0$ y $A=1$, $B=-1$ y $C=1$, podemos escribir $\pi:x-y+z+D=0 \quad \quad (3) $. Y como sabemos que $O(0,0,0)$ es un punto de $\pi$, deducimos ( sustituyendo las coordenadas de $O$ en la ecuación (3) ) que $D=0$, con lo cual vemos que la ecuación del plano pedido es $$\pi:x-y+z=0$$
La ecuación de la recta (2) también podemos expresarla en forma implícita (como la intersección de dos planos): $$s:\left\{\begin{matrix}x=2-y\\x=z-1\end{matrix}\right.$$ que junto con la ecuación del plano $\pi:x-y+z=0$ nos lleva al sistema de ecuaciones $$\left\{\begin{matrix}x&-&y&+&z&=&0 \\ x&+&y&&&=&2 \\ x&&&-&z&=&-1\end{matrix}\right. \sim \left\{\begin{matrix}x&-&y&+&z&=&0 \\ &&2y&-&z&=&2 \\ &&y&-&2z&=&-1\end{matrix}\right.\sim$$
$$\sim \left\{\begin{matrix}x&-&y&+&z&=&0 \\ &&2y&-&z&=&2 \\ &&&&3z&=&4\end{matrix}\right.$$ con lo cual, despejando de la última ecuación, $z=\dfrac{4}{3}$; sustituyendo en la segunda, $y=\dfrac{5}{3}$; y, sustituyendo estos dos valores en la primera ecuación, $x=\dfrac{1}{3}$. Así pues el punto de corte viene dado por $( \dfrac{1}{3}\,,\,\dfrac{5}{3}\,,\,\dfrac{4}{3})$
$\square$
Cálculo con matrices y determinantes
ENUNCIADO. Dadas las matrices $P=\begin{pmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{pmatrix}$ y $J=\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}$ se pide:
a) Determinar $P^{-1}$
b) Determinar $B^{-1}$, siendo $B=P^{-1}J^{-1}$
c) Calcular el determinante de $A^2$, siendo $A=PJP^{-1}$
SOLUCIÓN.
a)
Una condición necesaria y suficiente para que una matriz cuadrada tenga asociada una matriz inversa es que su determinante sea distinto de cero. Veamos si lo es: $\text{det}(P)=\begin{vmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{vmatrix}=-1$, luego $P$ tiene inversa. Sugiero que se utilice el método de Gauss-Jordan tal como se muestra en [este otro ejercicio rutinario], obteniendo $$P^{-1}=\begin{pmatrix}2&1&-2\\ 2&0&1 \\ -5&-1&4\end{pmatrix}$$
b)
Notemos que $B=P^{-1}J^{-1}=(JP)^{-1}$ y, por tanto, $B^{-1}=\left((JP)^{-1}\right)^{-1}=JP=\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}\begin{pmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{pmatrix}=\begin{pmatrix}-1&-2&-1\\ 6&4&4 \\ 2&3&2\end{pmatrix}$
c)
$A^2=(PJP^{-1})^2=(PJP^{-1})(PJP^{-1})=PJ(P^{-1}P)JP^{-1}=PJIJP^{-1}=$
$=PJJP^{-1}=PJ^2P^{-1}=P(J^2P^{-1})\quad \quad \quad (1)$
Entonces,
$J^2=\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}=\begin{pmatrix}1&0&0\\ 0&4&0 \\ 0&0&1\end{pmatrix}$
y por tanto $J^2P^{-1}=\begin{pmatrix}1&0&0\\ 0&4&0 \\ 0&0&1\end{pmatrix}\begin{pmatrix}2&1&-2\\ 2&0&1 \\ -5&-1&4\end{pmatrix}=\begin{pmatrix}2&1&-2\\ 8&0&-4 \\ -5&-1&4\end{pmatrix}$ luego, de (1), llegamos a $$A^2=\begin{pmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{pmatrix}\begin{pmatrix}2&1&-2\\ 8&0&-4 \\ -5&-1&4\end{pmatrix}=\begin{pmatrix}13&0&-6\\ 12&1&-6 \\ 18&0&-8\end{pmatrix}$$ Con lo cual $$\text{det}(A^2)=\begin{vmatrix}13&0&-6\\ 12&1&-6 \\ 18&0&-8\end{vmatrix}=4$$
$\square$
a) Determinar $P^{-1}$
b) Determinar $B^{-1}$, siendo $B=P^{-1}J^{-1}$
c) Calcular el determinante de $A^2$, siendo $A=PJP^{-1}$
SOLUCIÓN.
a)
Una condición necesaria y suficiente para que una matriz cuadrada tenga asociada una matriz inversa es que su determinante sea distinto de cero. Veamos si lo es: $\text{det}(P)=\begin{vmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{vmatrix}=-1$, luego $P$ tiene inversa. Sugiero que se utilice el método de Gauss-Jordan tal como se muestra en [este otro ejercicio rutinario], obteniendo $$P^{-1}=\begin{pmatrix}2&1&-2\\ 2&0&1 \\ -5&-1&4\end{pmatrix}$$
b)
Notemos que $B=P^{-1}J^{-1}=(JP)^{-1}$ y, por tanto, $B^{-1}=\left((JP)^{-1}\right)^{-1}=JP=\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}\begin{pmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{pmatrix}=\begin{pmatrix}-1&-2&-1\\ 6&4&4 \\ 2&3&2\end{pmatrix}$
c)
$A^2=(PJP^{-1})^2=(PJP^{-1})(PJP^{-1})=PJ(P^{-1}P)JP^{-1}=PJIJP^{-1}=$
$=PJJP^{-1}=PJ^2P^{-1}=P(J^2P^{-1})\quad \quad \quad (1)$
Entonces,
$J^2=\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}\begin{pmatrix}-1&0&0\\ 0&2&0 \\ 0&0&1\end{pmatrix}=\begin{pmatrix}1&0&0\\ 0&4&0 \\ 0&0&1\end{pmatrix}$
y por tanto $J^2P^{-1}=\begin{pmatrix}1&0&0\\ 0&4&0 \\ 0&0&1\end{pmatrix}\begin{pmatrix}2&1&-2\\ 2&0&1 \\ -5&-1&4\end{pmatrix}=\begin{pmatrix}2&1&-2\\ 8&0&-4 \\ -5&-1&4\end{pmatrix}$ luego, de (1), llegamos a $$A^2=\begin{pmatrix}1&2&1\\ 3&2&2 \\ 2&3&2\end{pmatrix}\begin{pmatrix}2&1&-2\\ 8&0&-4 \\ -5&-1&4\end{pmatrix}=\begin{pmatrix}13&0&-6\\ 12&1&-6 \\ 18&0&-8\end{pmatrix}$$ Con lo cual $$\text{det}(A^2)=\begin{vmatrix}13&0&-6\\ 12&1&-6 \\ 18&0&-8\end{vmatrix}=4$$
$\square$
Análisis de funciones y cálculo integral
ENUNCIADO. Dadas las funciones $f(x)=\dfrac{2}{x}$ y $g(x)=\sin\,x$, se pide:
a) Calcular $\displaystyle \lim_{x\rightarrow 0}\,(f(x)-\dfrac{2}{g(x)})$
b) Calcular la ecuación de la recta tangente a la curva $y=f(x)$ en el punto $(\dfrac{1}{2}\,,\,4)$
c) Calcular el área delimitada por la curva $y=f(x)$ y la recta $y=-x+3$
SOLUCIÓN.
a)
Cuando $x \rightarrow 0$, $x \sim \sin\,x$ ( son infinitésimos equivalentes ), luego $$\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{\sin\,x})=2\,\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{x})=0$$
b)En $x=\dfrac{1}{2}$ podemos determinar la recta tangente a la gráfica de la función $f(x)$ pues en ese punto la función es derivable. Sea la ecuación en forma explícita de la recta tangente $t:y=mx+k$ en dicho punto. Vamos a determinar los valores de los coeficientes $m$ ( pendiente de la recta ) y $k$ ( ordenada en el origen ).
$m\overset{\text{def}}{=}f'(1/2)=((\dfrac{2}{x})')|_{x=1/2}=(-\dfrac{2}{x^2})|_{x=1/2}=-8$, con lo cual podemos escribir $t:y=-8\,x+k$, veamos ahora, cuál es el valor de $k$: como en $x=1/2$ se tiene que cumplir que $f(1/2)=(-8\,x+k)_{x=1/2}$, vemos que $f(1/2)=-8\cdot \dfrac{1}{2} +k$, luego $k=f(1/2)+4$, esto es, $k=(\dfrac{2}{1/2})+4=8$. Así concluimos que la ecuación de la recta tangente pedida es $t:y=-8\,x+8$
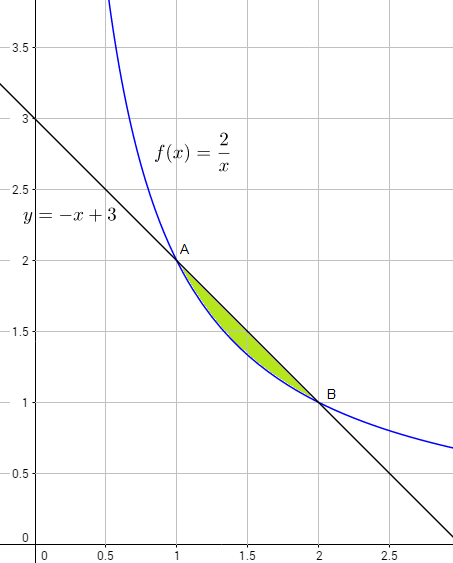
c) El siguiente gráfico ( las gráficas de las dos funciones inciden en el primer cuadrante ) ayuda a visualizar el área pedida
Entonces, $$\text{Área}=\displaystyle \int_{x_A}^{x_B}\,((-x+3)-f(x))\,dx=\int_{x_A}^{x_B}\,((-x+3)-\dfrac{2}{x})\,dx \quad \quad (1)$$ Necesitamos conocer los límite de integración, que son las abscisas de los puntos de intersección $A$ y $B$, y que se calculan resolviendo la ecuación $$\dfrac{2}{x}=-x+3$$ esto es $$x^2-3x+2=0\Leftrightarrow x=\dfrac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2 \cdot 1}=\dfrac{3\pm 1}{2}=\left\{\begin{matrix}2 \\ 1 \end{matrix}\right.$$ con lo cual $x_A=1$ y $x_B=2$
Así, de (1), $$\text{Área}=\displaystyle \int_{1}^{2}\,\dfrac{-x^2+3x-2}{x}\,dx=\int_{1}^{2}\,(-x+3-\dfrac{2}{x})\,dx=\displaystyle -\dfrac{1}{2}\,\left[x^2\right]_{1}^{2}+3\,\left[x\right]_{1}^{2}-2\,\left[\ln\,x\right]_{1}^{2}$$
$=-\dfrac{1}{2}\cdot (4-1)+3\cdot (2-1)-2\cdot (\ln\,2-\ln\,1)=-\dfrac{3}{2}+3-2\,\ln\,2=$
$=(\dfrac{3}{2}-2\,\ln\,2) \; \text{u.a.} \approx 0,1137 \; \text{u.a.}$
$\square$
a) Calcular $\displaystyle \lim_{x\rightarrow 0}\,(f(x)-\dfrac{2}{g(x)})$
b) Calcular la ecuación de la recta tangente a la curva $y=f(x)$ en el punto $(\dfrac{1}{2}\,,\,4)$
c) Calcular el área delimitada por la curva $y=f(x)$ y la recta $y=-x+3$
SOLUCIÓN.
a)
Cuando $x \rightarrow 0$, $x \sim \sin\,x$ ( son infinitésimos equivalentes ), luego $$\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{\sin\,x})=2\,\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{x})=0$$
b)En $x=\dfrac{1}{2}$ podemos determinar la recta tangente a la gráfica de la función $f(x)$ pues en ese punto la función es derivable. Sea la ecuación en forma explícita de la recta tangente $t:y=mx+k$ en dicho punto. Vamos a determinar los valores de los coeficientes $m$ ( pendiente de la recta ) y $k$ ( ordenada en el origen ).
$m\overset{\text{def}}{=}f'(1/2)=((\dfrac{2}{x})')|_{x=1/2}=(-\dfrac{2}{x^2})|_{x=1/2}=-8$, con lo cual podemos escribir $t:y=-8\,x+k$, veamos ahora, cuál es el valor de $k$: como en $x=1/2$ se tiene que cumplir que $f(1/2)=(-8\,x+k)_{x=1/2}$, vemos que $f(1/2)=-8\cdot \dfrac{1}{2} +k$, luego $k=f(1/2)+4$, esto es, $k=(\dfrac{2}{1/2})+4=8$. Así concluimos que la ecuación de la recta tangente pedida es $t:y=-8\,x+8$
c) El siguiente gráfico ( las gráficas de las dos funciones inciden en el primer cuadrante ) ayuda a visualizar el área pedida
Entonces, $$\text{Área}=\displaystyle \int_{x_A}^{x_B}\,((-x+3)-f(x))\,dx=\int_{x_A}^{x_B}\,((-x+3)-\dfrac{2}{x})\,dx \quad \quad (1)$$ Necesitamos conocer los límite de integración, que son las abscisas de los puntos de intersección $A$ y $B$, y que se calculan resolviendo la ecuación $$\dfrac{2}{x}=-x+3$$ esto es $$x^2-3x+2=0\Leftrightarrow x=\dfrac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2 \cdot 1}=\dfrac{3\pm 1}{2}=\left\{\begin{matrix}2 \\ 1 \end{matrix}\right.$$ con lo cual $x_A=1$ y $x_B=2$
Así, de (1), $$\text{Área}=\displaystyle \int_{1}^{2}\,\dfrac{-x^2+3x-2}{x}\,dx=\int_{1}^{2}\,(-x+3-\dfrac{2}{x})\,dx=\displaystyle -\dfrac{1}{2}\,\left[x^2\right]_{1}^{2}+3\,\left[x\right]_{1}^{2}-2\,\left[\ln\,x\right]_{1}^{2}$$
$=-\dfrac{1}{2}\cdot (4-1)+3\cdot (2-1)-2\cdot (\ln\,2-\ln\,1)=-\dfrac{3}{2}+3-2\,\ln\,2=$
$=(\dfrac{3}{2}-2\,\ln\,2) \; \text{u.a.} \approx 0,1137 \; \text{u.a.}$
$\square$
Análisis y cálculo
ENUNCIADO. Dada la función $f(x)=\dfrac{x^2+x+6}{x-2}$, se pide:
a) Determínese el dominio de definición y las rectas asíntotas de la función
b) Calcúlese el límite $\displaystyle \lim_{x \rightarrow \infty}\,\dfrac{f(x)}{x}$
c) Calcúlese $\displaystyle \int_{3}^{5}\,f(x)\,dx$
SOLUCIÓN.
a)
Recordemos que $\text{Dom}\,f\overset{\text{def}}{=}\{x\in \mathbb{R}: f(x)\in \mathbb{R}\}$. Veamos, primero, si se puede factorizar el polinomio del numerado $x^2+x+6$; démonos cuenta de que no tiene raíces ( reales ) pues el discriminante de la ecuación de segundo grado $1-4\cdot 6\cdot 1 \prec 0$, luego no tiene raíces en $\mathbb{R}$, luego $x^2+x+6$ no puede factorizarse. Así, el único número real que no tiene imagen por $f$ es $x=2$, pues este valor anula el denominador ( y no el numerador ) dando como resultado un infinito. Por consiguiente, $\text{Dom}\,f=\mathbb{R}\setminus\{2\}$
Por lo dicho anteriormente, sabemos que la función dada tiene un (recta) asíntota vertical, de ecuación $\text{a.v.}:x=2$. A continuación, examinemos si tiene (rectas) asíntotas oblicuas, que, desde luego, son del tipo: $a.o.:y=mx+k$. Primero, calcularemos la pendiente de esta(s) recta(s) $$m\overset{\text{def}}{=}\displaystyle \lim_{x\rightarrow \infty}\,f'(x)=\lim_{x\rightarrow \infty}\,\dfrac{f(x)}{x}=\lim_{x\rightarrow \infty}\,\dfrac{x^2+x+6}{x^2-2x}=1 \quad \quad (1)$$ A continuación, calcularemos el valor de la ordenada en el origen $$k\overset{\text{def}}{=}\displaystyle \lim_{x\rightarrow \infty}\,(f(x)-mx)=\lim_{x\rightarrow \infty}\,(f(x)-x)=\lim_{x\rightarrow \infty}\,\dfrac{3x+6}{x-2}=3$$ Así pues hay una sóla asíntota oblicua: $a.o.:y=x+3$. Y como $m\neq 0$, no la función no tiene asíntotas horizontales )
b)
En (1) ya se ha calculado este límite, que es igual a $1$
c)
Calculemos una primitiva de $f(x)$: $$F(x)=\int\,f(x)\,dx=\int\,\dfrac{x^2+x+6}{x-2}\,dx \quad \quad (1)$$ Haciendo el cambio de variable $t=x-2$, obtenemos $dt=(x-2)'\,dx=dx$; entonces $x=t+2$, por tanto (1) nos queda $$\int\,\dfrac{(t+2)^2+(t+2)+6}{t}\,dt=\int\,\dfrac{t^2+5t+12}{t}\,dt=\int\,t\,dt+5\,\int\,dt+12\,\int\,\dfrac{dt}{t}=$$ $$=\dfrac{1}{2}\,t^2+5\,t+12\,\ln\,|t|$$ Vamos ahora a aplicar la regla de Barrow para calcular la integral definida, pero para ello debemos tener en cuenta cuáles son los nuevos límites de integración ( con el cambio de variable ): cuando $x=3$, $t=1$; y para $x=5$, $t=3$, luego $$\int_{3}^{5}\,f(x)\,dx=\left[\dfrac{1}{2}\,t^2+5\,t+12\,\ln\,|t|\right]_{1}^{3}=$$ $$=(\dfrac{1}{2}\cdot 3^2+5\cdot 3+12\cdot \ln\,3)-(\dfrac{1}{2}\cdot 1^2+5\cdot 1+12\cdot \ln\,1)=12\cdot \ln\,3+14$$
$\square$
a) Determínese el dominio de definición y las rectas asíntotas de la función
b) Calcúlese el límite $\displaystyle \lim_{x \rightarrow \infty}\,\dfrac{f(x)}{x}$
c) Calcúlese $\displaystyle \int_{3}^{5}\,f(x)\,dx$
SOLUCIÓN.
a)
Recordemos que $\text{Dom}\,f\overset{\text{def}}{=}\{x\in \mathbb{R}: f(x)\in \mathbb{R}\}$. Veamos, primero, si se puede factorizar el polinomio del numerado $x^2+x+6$; démonos cuenta de que no tiene raíces ( reales ) pues el discriminante de la ecuación de segundo grado $1-4\cdot 6\cdot 1 \prec 0$, luego no tiene raíces en $\mathbb{R}$, luego $x^2+x+6$ no puede factorizarse. Así, el único número real que no tiene imagen por $f$ es $x=2$, pues este valor anula el denominador ( y no el numerador ) dando como resultado un infinito. Por consiguiente, $\text{Dom}\,f=\mathbb{R}\setminus\{2\}$
Por lo dicho anteriormente, sabemos que la función dada tiene un (recta) asíntota vertical, de ecuación $\text{a.v.}:x=2$. A continuación, examinemos si tiene (rectas) asíntotas oblicuas, que, desde luego, son del tipo: $a.o.:y=mx+k$. Primero, calcularemos la pendiente de esta(s) recta(s) $$m\overset{\text{def}}{=}\displaystyle \lim_{x\rightarrow \infty}\,f'(x)=\lim_{x\rightarrow \infty}\,\dfrac{f(x)}{x}=\lim_{x\rightarrow \infty}\,\dfrac{x^2+x+6}{x^2-2x}=1 \quad \quad (1)$$ A continuación, calcularemos el valor de la ordenada en el origen $$k\overset{\text{def}}{=}\displaystyle \lim_{x\rightarrow \infty}\,(f(x)-mx)=\lim_{x\rightarrow \infty}\,(f(x)-x)=\lim_{x\rightarrow \infty}\,\dfrac{3x+6}{x-2}=3$$ Así pues hay una sóla asíntota oblicua: $a.o.:y=x+3$. Y como $m\neq 0$, no la función no tiene asíntotas horizontales )
b)
En (1) ya se ha calculado este límite, que es igual a $1$
c)
Calculemos una primitiva de $f(x)$: $$F(x)=\int\,f(x)\,dx=\int\,\dfrac{x^2+x+6}{x-2}\,dx \quad \quad (1)$$ Haciendo el cambio de variable $t=x-2$, obtenemos $dt=(x-2)'\,dx=dx$; entonces $x=t+2$, por tanto (1) nos queda $$\int\,\dfrac{(t+2)^2+(t+2)+6}{t}\,dt=\int\,\dfrac{t^2+5t+12}{t}\,dt=\int\,t\,dt+5\,\int\,dt+12\,\int\,\dfrac{dt}{t}=$$ $$=\dfrac{1}{2}\,t^2+5\,t+12\,\ln\,|t|$$ Vamos ahora a aplicar la regla de Barrow para calcular la integral definida, pero para ello debemos tener en cuenta cuáles son los nuevos límites de integración ( con el cambio de variable ): cuando $x=3$, $t=1$; y para $x=5$, $t=3$, luego $$\int_{3}^{5}\,f(x)\,dx=\left[\dfrac{1}{2}\,t^2+5\,t+12\,\ln\,|t|\right]_{1}^{3}=$$ $$=(\dfrac{1}{2}\cdot 3^2+5\cdot 3+12\cdot \ln\,3)-(\dfrac{1}{2}\cdot 1^2+5\cdot 1+12\cdot \ln\,1)=12\cdot \ln\,3+14$$
$\square$
Análisis de funciones
ENUNCIADO. Se administra una medicina a un enfermo y $t$ horas después la concentración en sangre del principio activo viene dada por $c(t)=t\,e^{-t/2}$ ( en miligramos por mililitro ). Determínese el valor máximo de la concentración e indique en qué momento se alcanza dicho valor máximo. Sabiendo que la máxima concentración sin peligro para el paciente es de $1$ miligramo por mililitro, señale si en algún momento hay riesgo.
SOLUCIÓN.
Imponiendo la condición necesaria de extremos relativos, $c'(t)=0$, y siendo $c'(t)=e^{-t/2}\,(1-\dfrac{t}{2})$, dichos extremos han de ser solución de la ecuación $e^{-t/2}\,(1-\dfrac{t}{2})=0$, encontrando un único valor como solución: $t=2$ horas. Para ver si corresponde a un máximo local, utilizaremos el criterio del signo de la segunda derivada, $c''(t)=-\dfrac{1}{2}\,e^{-t/2}\,((2-\dfrac{t}{2})$ ( se ruega al lector que reproduzca los cálculos omitidos ); así, $c''(2)=-\dfrac{1}{2e} \prec 0$, de lo cual deducimos que $t=2$ es la abscisa de un máximo local, y teniendo en cuenta que $\text{Dom}\,c(t)=[0\,,\,+\infty)\subset \mathbb{R}$ y $\displaystyle \lim_{t\rightarrow +\infty}\,c(t)=0$, dicho máximo es también el máximo absoluto.
La máxima concentración en sangre del principio activo es pues $c(2)=2\cdot e^{-2/2}=\dfrac{2}{e} \approx 0,7 \; \dfrac{\text{mg}}{\text{ml}}\prec 1\; \dfrac{\text{mg}}{\text{ml}}$, luego no habrá ningún momento de riesgo para el paciente. $\square$
SOLUCIÓN.
Imponiendo la condición necesaria de extremos relativos, $c'(t)=0$, y siendo $c'(t)=e^{-t/2}\,(1-\dfrac{t}{2})$, dichos extremos han de ser solución de la ecuación $e^{-t/2}\,(1-\dfrac{t}{2})=0$, encontrando un único valor como solución: $t=2$ horas. Para ver si corresponde a un máximo local, utilizaremos el criterio del signo de la segunda derivada, $c''(t)=-\dfrac{1}{2}\,e^{-t/2}\,((2-\dfrac{t}{2})$ ( se ruega al lector que reproduzca los cálculos omitidos ); así, $c''(2)=-\dfrac{1}{2e} \prec 0$, de lo cual deducimos que $t=2$ es la abscisa de un máximo local, y teniendo en cuenta que $\text{Dom}\,c(t)=[0\,,\,+\infty)\subset \mathbb{R}$ y $\displaystyle \lim_{t\rightarrow +\infty}\,c(t)=0$, dicho máximo es también el máximo absoluto.
La máxima concentración en sangre del principio activo es pues $c(2)=2\cdot e^{-2/2}=\dfrac{2}{e} \approx 0,7 \; \dfrac{\text{mg}}{\text{ml}}\prec 1\; \dfrac{\text{mg}}{\text{ml}}$, luego no habrá ningún momento de riesgo para el paciente. $\square$
Geometría analítica en el espacio R^3
ENUNCIADO. Dados los puntos $P(1,-2,1)$, $Q(-4,0,1)$ , $R(-3,1,2)$, $S(0,-3,0)$. Se pide:
a) Hallar la ecuación del plano que contiene a $P$, $Q$ y $R$
b) Estudiar la posición relativa de la recta $r$ que pasa por los puntos $P$ y $Q$, y la recta $s$ que pasa por los puntos $R$ y $S$
c) Hallar el área del triángulo cuyos vértices son los puntos $P$, $Q$ y $R$
SOLUCIÓN.
a) Denotemos por $\pi$ al plano pedido. Un vector perpendicular a $\pi$ es $\vec{PQ}\times \vec{PR}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\-5&2&0\\-4&3&1\end{vmatrix}=2\,\vec{i}+5\,\vec{j}-7\,\vec{k}=(2,5,-7)$, luego $\pi:2x+5y-7z+D=0$. Para determinar $D$ tendremos en cuenta que $P(1,-2,1)$ está en $\pi$, por lo que deberá cumplirse que $2\cdot 1+5\cdot (-2)-7\cdot 1+D=0$ de donde despejando $D$, obtenemos $D=15$. Así pues, $\pi:2x+5y-7z+15=0$
b) Un vector director de $r$ es $\vec{PQ}=(-5,2,0)$, luego $$r:\dfrac{x-1}{-5}=\dfrac{y-(-2)}{2}=\dfrac{z-1}{0} \Leftrightarrow \left\{\begin{matrix} \dfrac{x-1}{-5}=\dfrac{y+2}{2} \\ \dfrac{x-1}{-5}=\dfrac{z-1}{0}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2x+5y=-8 \\ z-1=0 \end{matrix}\right.\quad \quad (1)$$
Un vector director de $s$ es $\vec{RS}=(0-(-3),-3-1,0-2)=(3,-4,-2)$, luego $$r:\dfrac{x-(-3)}{3}=\dfrac{y-1}{-4}=\dfrac{z-2}{-2} \Leftrightarrow \left\{\begin{matrix} \dfrac{x+3}{3}=\dfrac{z-2}{-2} \\ \dfrac{x+3}{3}=\dfrac{y-1}{-4}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2x+3z=0 \\ 4x+3y=-9 \end{matrix}\right.\quad \quad (2)$$
Resolviendo ( muy fácilmente ) el sistema de ecuaciones formado por las dos ecuaciones de (1) y las dos ecuaciones de (2) $\left\{\begin{matrix}2x&+&5y&&&=&-8 \\ &&&&z&=&1\\ 2x&&&+&3z&=&0 \\ 4x&+&3y&&&=&-9\end{matrix}\right.$ obtenemos como solución ( resulta ser un sistema compatible determinado y por tanto las rectas se cortan ) $\left\{\begin{matrix}x&&&&&=&-\dfrac{3}{2} \\ &&y&&&=&-1\\ &&&&z&=&1 \end{matrix}\right.$ que son las coordenadas del punto de intersección de $r$ y $s$
c)
Recordemos que $\text{Área}\overset{\text{def}}{=}\left|\vec{PQ} \times \vec{PR}\right\|$ y como [ apartado a) ] $\vec{PQ} \times \vec{PR}=(2,5,-7)$, $\text{Área}=\left\|\sqrt{2^2+5^2+(-7)^2}\right\|=\left|\sqrt{78}\right|$ u.a.
$\square$
a) Hallar la ecuación del plano que contiene a $P$, $Q$ y $R$
b) Estudiar la posición relativa de la recta $r$ que pasa por los puntos $P$ y $Q$, y la recta $s$ que pasa por los puntos $R$ y $S$
c) Hallar el área del triángulo cuyos vértices son los puntos $P$, $Q$ y $R$
SOLUCIÓN.
a) Denotemos por $\pi$ al plano pedido. Un vector perpendicular a $\pi$ es $\vec{PQ}\times \vec{PR}=\begin{vmatrix}\vec{i}&\vec{j}&\vec{k}\\-5&2&0\\-4&3&1\end{vmatrix}=2\,\vec{i}+5\,\vec{j}-7\,\vec{k}=(2,5,-7)$, luego $\pi:2x+5y-7z+D=0$. Para determinar $D$ tendremos en cuenta que $P(1,-2,1)$ está en $\pi$, por lo que deberá cumplirse que $2\cdot 1+5\cdot (-2)-7\cdot 1+D=0$ de donde despejando $D$, obtenemos $D=15$. Así pues, $\pi:2x+5y-7z+15=0$
b) Un vector director de $r$ es $\vec{PQ}=(-5,2,0)$, luego $$r:\dfrac{x-1}{-5}=\dfrac{y-(-2)}{2}=\dfrac{z-1}{0} \Leftrightarrow \left\{\begin{matrix} \dfrac{x-1}{-5}=\dfrac{y+2}{2} \\ \dfrac{x-1}{-5}=\dfrac{z-1}{0}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2x+5y=-8 \\ z-1=0 \end{matrix}\right.\quad \quad (1)$$
Un vector director de $s$ es $\vec{RS}=(0-(-3),-3-1,0-2)=(3,-4,-2)$, luego $$r:\dfrac{x-(-3)}{3}=\dfrac{y-1}{-4}=\dfrac{z-2}{-2} \Leftrightarrow \left\{\begin{matrix} \dfrac{x+3}{3}=\dfrac{z-2}{-2} \\ \dfrac{x+3}{3}=\dfrac{y-1}{-4}\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} 2x+3z=0 \\ 4x+3y=-9 \end{matrix}\right.\quad \quad (2)$$
Resolviendo ( muy fácilmente ) el sistema de ecuaciones formado por las dos ecuaciones de (1) y las dos ecuaciones de (2) $\left\{\begin{matrix}2x&+&5y&&&=&-8 \\ &&&&z&=&1\\ 2x&&&+&3z&=&0 \\ 4x&+&3y&&&=&-9\end{matrix}\right.$ obtenemos como solución ( resulta ser un sistema compatible determinado y por tanto las rectas se cortan ) $\left\{\begin{matrix}x&&&&&=&-\dfrac{3}{2} \\ &&y&&&=&-1\\ &&&&z&=&1 \end{matrix}\right.$ que son las coordenadas del punto de intersección de $r$ y $s$
c)
Recordemos que $\text{Área}\overset{\text{def}}{=}\left|\vec{PQ} \times \vec{PR}\right\|$ y como [ apartado a) ] $\vec{PQ} \times \vec{PR}=(2,5,-7)$, $\text{Área}=\left\|\sqrt{2^2+5^2+(-7)^2}\right\|=\left|\sqrt{78}\right|$ u.a.
$\square$
Discutir en función de los valores del parámetro y resolver cuando proceda el siguiente sistema de ecuaciones
ENUNCIADO. Dado el siguiente sistema de ecuaciones $$\begin{matrix} 2\,x&+&a\,y&+&z&=&a \\ x&-&4\,y&+&(a+1)\,z&=&1 \\ &&4\,y&-&a\,z&=&0\end{matrix}$$ Se pide:
a) Discutirlo en función de los valores del parámetro $a$
b) Resolver el sistema para $a=1$
c) Resolver el sistema para $a=2$
SOLUCIÓN.
a)
La matriz de los coeficientes del sistema es $A=\begin{pmatrix}2&a&1\\1&-4&(a+1)\\ 0&4&-a\end{pmatrix}$ y la matriz ampliada $(A|b)=\begin{pmatrix}2&a&1&a\\1&-4&(a+1)&1\\ 0&4&-a&0\end{pmatrix}$
Observemos que $\text{det}(A)=\begin{vmatrix}2&a&1\\1&-4&(a+1)\\ 0&4&-a\end{vmatrix}=a^2-4 = 0 \Leftrightarrow a=\pm 2$. Entonces, si $a \in \{-2\,,\,2\}$, $\text{rango}(A)=2$, puesto que en estas condiciones no puede ser igual a $3$, y $A$ tiene un menor de orden $2$ distinto de $0$ ( en efecto, $\begin{vmatrix}1&-4\\0&4\end{vmatrix}=4\neq 0$ )
Veamos ahora cuáles son los posibles rangos de la matriz ampliada $(A|b)$, para ello emplearemos el método del orlado del menor complementario no nulo que hemos encontrado. Así, aparecen dos menores de orden $3$ que son:
$\Delta_1=\begin{vmatrix}2&a&1\\1&-4&(a+1)\\ 0&4&-a\end{vmatrix}$, que es el de la matriz de los coeficientes y ya hemos analizado
y
$\Delta_2=\begin{vmatrix}2&a&a\\1&-4&1\\ 0&4&0\end{vmatrix}=0 \Leftrightarrow 4\,(a-2)=0 \Leftrightarrow a=2$
Entonces, por el teorema de Rouché-Fröbenius, tenemos los siguientes casos:
i) Si $a=-2$, $r=\text{rango}(A)=2$ y $\text{rango}(A|b)=3$ ( ya que hay un menor de orden $3$, $\Delta_2$, que no se anula para esos valores ), y, al no coincidir los rangos, el sistema es incompatible
ii) Si $a=2$, $r=\text{rango}(A)=2$ y $\text{rango}(A|b)=2$ ( ya que los menores de orden $3$ del orlado, $\Delta_1$ como $\Delta_2$, son nulos ); entonces $r=2\prec n=3$, luego el sistema es compatible indeterminado con $n-r=3-2=1$ variable secundaria
iii) Para cualquier otro valor de $a$, $\text{rango}(A|b)=\text{rango}(A)=3=n$ y el sistema es compatible determinado
b)
Para $a=1$ estamos en el caso (ii) y el sistema es compatible determinado. Queda así: $$\left\{\begin{matrix} 2\,x&+&y&+&z&=&1 \\ x&-&4\,y&+&2\,z&=&1 \\ &&4\,y&-&z&=&0\end{matrix}\right.$$ al reducirlo por Gauss nos queda el sistema equivalente $$\left\{\begin{matrix} 2\,x&+&y&+&z&=&1 \\ &&9\,y&-&3\,z&=&-1 \\ &&&&3\,z&=&4\end{matrix}\right.$$ así que, despejando $z$ de la última ecuación y sustituyendo de forma regresiva, llegamos a $$\left\{\begin{matrix} x&&&&&=&-\dfrac{1}{3} \\ &&y&&&=&\dfrac{1}{3} \\ &&&&z&=&\dfrac{4}{3}\end{matrix}\right.$$
c)
Para $a=2$ estamos en el caso (iii) y el sistema es compatible indeterminado con una variable secundaria. Queda así: $$\left\{\begin{matrix} 2\,x&+&\,2y&+&z&=&2 \\ x&-&4\,y&+&3\,z&=&1 \\ &&4\,y&-&2\,z&=&0\end{matrix}\right.$$ Reduciendo por Gauss llegamos al siguiente sistema equivalente $$\left\{\begin{matrix} 2\,x&+&\,2y&+&z&=&2 \\ &&2\,y&-&z&=&0 \end{matrix}\right.$$
Tomando ahora $z$ como variable secundaria ( a la que llamamos $\lambda$ ) nos queda el siguiente sistema $$\left\{\begin{matrix} 2\,x&+&\,2y&=&2-\lambda \\ &&2\,y&=&\lambda \end{matrix}\right.$$ Despejando $y$ la segunda ecuación obtenemos $y=\dfrac{\lambda}{2}$ y sustituyendo este resultado en la primera llegamos a $2x+2\cdot \dfrac{\lambda}{2}=2-\lambda$, de donde $x=1-\lambda$. Así pues la solución viene dada por el conjunto de infinitos puntos del espacio $\mathbb{R}^3$ dados por $$\text{Solución}=\{(1-\lambda\,,\,\dfrac{\lambda}{2}\,,\,\lambda)\;\forall \lambda \in \mathbb{R}\}$$
$\square$
a) Discutirlo en función de los valores del parámetro $a$
b) Resolver el sistema para $a=1$
c) Resolver el sistema para $a=2$
SOLUCIÓN.
a)
La matriz de los coeficientes del sistema es $A=\begin{pmatrix}2&a&1\\1&-4&(a+1)\\ 0&4&-a\end{pmatrix}$ y la matriz ampliada $(A|b)=\begin{pmatrix}2&a&1&a\\1&-4&(a+1)&1\\ 0&4&-a&0\end{pmatrix}$
Observemos que $\text{det}(A)=\begin{vmatrix}2&a&1\\1&-4&(a+1)\\ 0&4&-a\end{vmatrix}=a^2-4 = 0 \Leftrightarrow a=\pm 2$. Entonces, si $a \in \{-2\,,\,2\}$, $\text{rango}(A)=2$, puesto que en estas condiciones no puede ser igual a $3$, y $A$ tiene un menor de orden $2$ distinto de $0$ ( en efecto, $\begin{vmatrix}1&-4\\0&4\end{vmatrix}=4\neq 0$ )
Veamos ahora cuáles son los posibles rangos de la matriz ampliada $(A|b)$, para ello emplearemos el método del orlado del menor complementario no nulo que hemos encontrado. Así, aparecen dos menores de orden $3$ que son:
$\Delta_1=\begin{vmatrix}2&a&1\\1&-4&(a+1)\\ 0&4&-a\end{vmatrix}$, que es el de la matriz de los coeficientes y ya hemos analizado
y
$\Delta_2=\begin{vmatrix}2&a&a\\1&-4&1\\ 0&4&0\end{vmatrix}=0 \Leftrightarrow 4\,(a-2)=0 \Leftrightarrow a=2$
Entonces, por el teorema de Rouché-Fröbenius, tenemos los siguientes casos:
i) Si $a=-2$, $r=\text{rango}(A)=2$ y $\text{rango}(A|b)=3$ ( ya que hay un menor de orden $3$, $\Delta_2$, que no se anula para esos valores ), y, al no coincidir los rangos, el sistema es incompatible
ii) Si $a=2$, $r=\text{rango}(A)=2$ y $\text{rango}(A|b)=2$ ( ya que los menores de orden $3$ del orlado, $\Delta_1$ como $\Delta_2$, son nulos ); entonces $r=2\prec n=3$, luego el sistema es compatible indeterminado con $n-r=3-2=1$ variable secundaria
iii) Para cualquier otro valor de $a$, $\text{rango}(A|b)=\text{rango}(A)=3=n$ y el sistema es compatible determinado
b)
Para $a=1$ estamos en el caso (ii) y el sistema es compatible determinado. Queda así: $$\left\{\begin{matrix} 2\,x&+&y&+&z&=&1 \\ x&-&4\,y&+&2\,z&=&1 \\ &&4\,y&-&z&=&0\end{matrix}\right.$$ al reducirlo por Gauss nos queda el sistema equivalente $$\left\{\begin{matrix} 2\,x&+&y&+&z&=&1 \\ &&9\,y&-&3\,z&=&-1 \\ &&&&3\,z&=&4\end{matrix}\right.$$ así que, despejando $z$ de la última ecuación y sustituyendo de forma regresiva, llegamos a $$\left\{\begin{matrix} x&&&&&=&-\dfrac{1}{3} \\ &&y&&&=&\dfrac{1}{3} \\ &&&&z&=&\dfrac{4}{3}\end{matrix}\right.$$
c)
Para $a=2$ estamos en el caso (iii) y el sistema es compatible indeterminado con una variable secundaria. Queda así: $$\left\{\begin{matrix} 2\,x&+&\,2y&+&z&=&2 \\ x&-&4\,y&+&3\,z&=&1 \\ &&4\,y&-&2\,z&=&0\end{matrix}\right.$$ Reduciendo por Gauss llegamos al siguiente sistema equivalente $$\left\{\begin{matrix} 2\,x&+&\,2y&+&z&=&2 \\ &&2\,y&-&z&=&0 \end{matrix}\right.$$
Tomando ahora $z$ como variable secundaria ( a la que llamamos $\lambda$ ) nos queda el siguiente sistema $$\left\{\begin{matrix} 2\,x&+&\,2y&=&2-\lambda \\ &&2\,y&=&\lambda \end{matrix}\right.$$ Despejando $y$ la segunda ecuación obtenemos $y=\dfrac{\lambda}{2}$ y sustituyendo este resultado en la primera llegamos a $2x+2\cdot \dfrac{\lambda}{2}=2-\lambda$, de donde $x=1-\lambda$. Así pues la solución viene dada por el conjunto de infinitos puntos del espacio $\mathbb{R}^3$ dados por $$\text{Solución}=\{(1-\lambda\,,\,\dfrac{\lambda}{2}\,,\,\lambda)\;\forall \lambda \in \mathbb{R}\}$$
$\square$
domingo, 18 de junio de 2017
Suscribirse a:
Entradas (Atom)