Análisis de funciones y cálculo integral

ENUNCIADO. Dadas las funciones $f(x)=\dfrac{2}{x}$ y $g(x)=\sin\,x$, se pide:
a) Calcular $\displaystyle \lim_{x\rightarrow 0}\,(f(x)-\dfrac{2}{g(x)})$
b) Calcular la ecuación de la recta tangente a la curva $y=f(x)$ en el punto $(\dfrac{1}{2}\,,\,4)$
c) Calcular el área delimitada por la curva $y=f(x)$ y la recta $y=-x+3$

SOLUCIÓN.
a)
Cuando $x \rightarrow 0$, $x \sim \sin\,x$ ( son infinitésimos equivalentes ), luego $$\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{\sin\,x})=2\,\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{x})=0$$

b)En $x=\dfrac{1}{2}$ podemos determinar la recta tangente a la gráfica de la función $f(x)$ pues en ese punto la función es derivable. Sea la ecuación en forma explícita de la recta tangente $t:y=mx+k$ en dicho punto. Vamos a determinar los valores de los coeficientes $m$ ( pendiente de la recta ) y $k$ ( ordenada en el origen ).

$m\overset{\text{def}}{=}f'(1/2)=((\dfrac{2}{x})')|_{x=1/2}=(-\dfrac{2}{x^2})|_{x=1/2}=-8$, con lo cual podemos escribir $t:y=-8\,x+k$, veamos ahora, cuál es el valor de $k$: como en $x=1/2$ se tiene que cumplir que $f(1/2)=(-8\,x+k)_{x=1/2}$, vemos que $f(1/2)=-8\cdot \dfrac{1}{2} +k$, luego $k=f(1/2)+4$, esto es, $k=(\dfrac{2}{1/2})+4=8$. Así concluimos que la ecuación de la recta tangente pedida es $t:y=-8\,x+8$

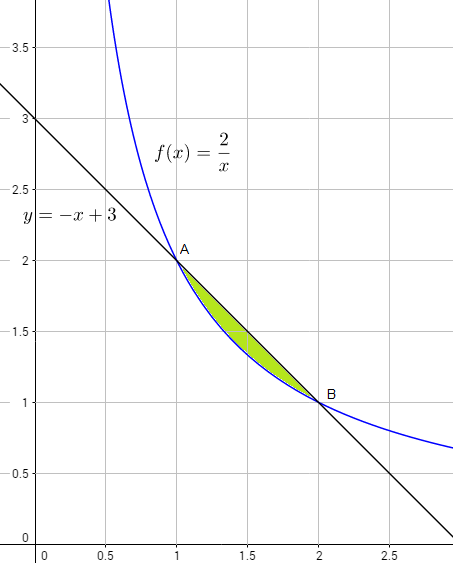
c) El siguiente gráfico ( las gráficas de las dos funciones inciden en el primer cuadrante ) ayuda a visualizar el área pedida

Entonces, $$\text{Área}=\displaystyle \int_{x_A}^{x_B}\,((-x+3)-f(x))\,dx=\int_{x_A}^{x_B}\,((-x+3)-\dfrac{2}{x})\,dx \quad \quad (1)$$ Necesitamos conocer los límite de integración, que son las abscisas de los puntos de intersección $A$ y $B$, y que se calculan resolviendo la ecuación $$\dfrac{2}{x}=-x+3$$ esto es $$x^2-3x+2=0\Leftrightarrow x=\dfrac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2 \cdot 1}=\dfrac{3\pm 1}{2}=\left\{\begin{matrix}2 \\ 1 \end{matrix}\right.$$ con lo cual $x_A=1$ y $x_B=2$

Así, de (1), $$\text{Área}=\displaystyle \int_{1}^{2}\,\dfrac{-x^2+3x-2}{x}\,dx=\int_{1}^{2}\,(-x+3-\dfrac{2}{x})\,dx=\displaystyle -\dfrac{1}{2}\,\left[x^2\right]_{1}^{2}+3\,\left[x\right]_{1}^{2}-2\,\left[\ln\,x\right]_{1}^{2}$$
$=-\dfrac{1}{2}\cdot (4-1)+3\cdot (2-1)-2\cdot (\ln\,2-\ln\,1)=-\dfrac{3}{2}+3-2\,\ln\,2=$
  $=(\dfrac{3}{2}-2\,\ln\,2) \; \text{u.a.} \approx 0,1137 \; \text{u.a.}$
$\square$