ENUNCIADO. Se considera la función real de una variable real $$f(x)=\dfrac{3x}{1-x^2}$$ Se pide:
a) Las rectas asíntotas, si las hubiese
b) Las abscisas de los puntos de inflexión, de haber alguno
c) El área del recinto limitado por la gráfica de la función y la recta $y=4x$
SOLUCIÓN.
a)
Asíntotas verticales:
Son del tipo $\text{a.v.}\equiv x=a$, donde $$\displaystyle \lim_{x \rightarrow a} \,f(x) = +\infty $$ o bien $$\displaystyle \lim_{x \rightarrow a }\,f(x) = -\infty$$ Estos valores de $a$ son los que anulan el denominador de la función ( sin anular el numerador ): $$1-x^2 =0 \Leftrightarrow x=\pm 1$$ pues, en efecto, se puede comprobar que $$\displaystyle \lim_{x\, \rightarrow\, -1^{-}}\,f(x)=+\infty\;\; \text{y} \;\; \displaystyle \lim_{x\, \rightarrow\, -1^{+}}\,f(x)=-\infty$$ y $$\displaystyle \lim_{x\, \rightarrow\, 1^{-}}\,f(x)=-\infty \;\; \text{y} \;\; \displaystyle \lim_{x\, \rightarrow\, 1^{+}}\,f(x)=+\infty$$ Así pues, encontramos dos asíntotas verticas: $$\text{a.v.}_1\equiv x=-1$$ y $$\text{a.v.}_2\equiv x=1$$
Asíntotas oblicuas:
Para encontrar las asíntotas oblicuas, $\text{a.o.}\equiv y=mx+k$, tendremos que calcular primero la pendiente, $m$:
$\displaystyle m\overset{\text{def}}{=} \lim_{x \rightarrow \pm \infty}\,f'(x) \overset{\text{def. equiv.}}{=} \lim_{x \rightarrow \pm \infty}\,\dfrac{f(x)}{x}=\lim_{x \rightarrow \pm \infty}\,\dfrac{3x}{x(1-x^2)}=$
$=\lim_{x\rightarrow \pm \infty}\,\dfrac{3}{1-x^2}=\dfrac{3}{1-\infty}=0$
A continuación, calculamos la ordenada en el origen, $k$:
$\displaystyle k\overset{\text{def}}{=}\lim_{x \rightarrow \pm \infty}\,\left( f(x)- m\,x\right)=\lim_{x \rightarrow \pm \infty} \left( f(x) - 0 \right)=\lim_{x\rightarrow \pm \infty}\,\dfrac{3x}{1-x^2}=0$ ( por ser el grado del polinomio del denominador mayor que el del numerador )
Encontramos pues una asíntota horizontal, como un caso particular de asíntota oblicua con pendiente nula: $$\text{a.h.}\equiv y=0$$
b)
Las abscisas de los puntos de inflexión son las raíces de la función segunda derivada ( condición necesaria ): $$f''(x)=0$$
Derivando una vez la función $f(x)$ obtenemos -- dejo al lector que reproduzca el cálculo rutinario --: $$f'(x)=3\cdot\dfrac{x^2+1}{(x^2-1)^2}$$
Nota: Démonos cuenta de que esta función no tiene raíces, pues el numerador no se anula para ningún valor de $x$, luego no hay extremos relativos
Y derivando, a su vez, la función primera derivada, llegamos a la función segunda derivada $$f''(x)=-6\cdot \dfrac{x\,(x^2+3)}{(x^2-1)^3}$$ Con lo cual $$-6\cdot \dfrac{x\,(x^2+3)}{(x^2-1)^3}\Leftrightarrow x=0$$
Si bien no se pide en el enunciado, un bosquejo de la gráfica de la función es el de la figura siguiente:
c)
Los puntos de corte de la gráfica de la función $y=4x$ con la gráfica de la función del integrando $f(x)=\dfrac{3x}{1-x^2}$ son las soluciones de la ecuación $$4x = \dfrac{3x}{1-x^2}$$ y, por tanto ( dejo al lector el cálculo elemental ), de $$4x^3-x=0$$ Sacando factor común de $x$ en el primer miembro, vemos que $$x\,(4x^2-1)=0 \Leftrightarrow \left\{\begin{matrix}x=0 \\ 4x^2-1=0 \Rightarrow x=\pm \,\dfrac{1}{2}\end{matrix}\right.$$ Tenemos por tanto tres puntos de corte, cuyas abscisas son $-1/2$, $0$ y $1/2$. Entonces,
$$\displaystyle \mathcal{Área}=\left| \int_{-1/2}^{0}\,f(x)\,dx \right| + \left| \int_{0}^{1/2}\,f(x)\,dx \right|\overset{\text{Barrow}}{=}|F(0)-F(-1/2)|+|F(1/2)-F(0)|$$
Calculando la integral definida de $f(x)$ encontraremos una función primitiva $F(x)$: $$\displaystyle \int\,\dfrac{3x}{1-x^2}\,dx = \dfrac{3}{2}\,\int\,\dfrac{2\,x\,dx}{1-x^2} = -\dfrac{3}{2}\,\int \,\dfrac{d(x^2-1)}{x^2-1} = -\dfrac{3}{2}\,\ln \, |x^2-1|+C$$ y eligiendo un valor cualquiera para la constante de integración, pongamos que $C:=0$, una función primitiva es $F(x)=-\dfrac{3}{2}\,\ln \, |x^2-1|$
Así pues,
$|F(0)-F(-1/2)|=\left|-\dfrac{3}{2}\cdot \ln\,|0-1|- (-\dfrac{3}{2})\cdot |\ln\,|(-1/2)^2-1|\right|=$
$=-\dfrac{3}{2}\,\ln\,(3/4)=\dfrac{3}{2}\,\ln\,(4/3)$
y
$|F(1/2)-F(0)|=\left|-\dfrac{3}{2}\cdot \ln\,|(1/2)^2-1|- (-\dfrac{3}{2})\cdot |\ln\,|0-1|\right|=$
$=-\dfrac{3}{2}\,\ln\,(3/4)=\dfrac{3}{2}\,\ln\,(4/3)$
por tanto,
$\mathcal{Área}=\dfrac{3}{2}\,\ln\,(4/3)+\dfrac{3}{2}\,\ln\,(4/3)=2\cdot \dfrac{3}{2}\,\ln\,(4/3)=$
$=3\,\ln\,(4/3)\;\text{unidades arbitrarias de área}$
$\square$
Un blog con cuestiones, ejercicios, problemas, aplicaciones y comentarios relacionados con los contenidos de Matemáticas del segundo curso de Bachillerato en las modalidades de Ciencias y Tecnología
Mostrando entradas con la etiqueta área de un recinto. Mostrar todas las entradas
Mostrando entradas con la etiqueta área de un recinto. Mostrar todas las entradas
sábado, 16 de junio de 2018
Análisis de funciones reales de una variable real
sábado, 9 de junio de 2018
Análisis de funciones
ENUNCIADO. Dada la función $f(x)=\dfrac{|x|}{\sqrt{x^2+9}}$ ( donde se toman sólo los valores positivos de la raíz cuadrada ), se pide:
a) Determinar, si existen, las asíntotas horizontales de $f(x)$
b) Calcular $f'(4)$
c) Hallar el área del recinto limitado por la gráfica de la función $y=f(x)$, el eje $Ox$, y las rectas $x=-1$ y $x=1$
SOLUCIÓN.
a) Determinar, si existen, las asíntotas horizontales de $f(x)$
b) Calcular $f'(4)$
c) Hallar el área del recinto limitado por la gráfica de la función $y=f(x)$, el eje $Ox$, y las rectas $x=-1$ y $x=1$
SOLUCIÓN.
Etiquetas:
análisis de funciones,
área de un recinto,
derivación,
integración
miércoles, 28 de junio de 2017
Análisis de funciones y cálculo integral
ENUNCIADO. Dadas las funciones $f(x)=\dfrac{2}{x}$ y $g(x)=\sin\,x$, se pide:
a) Calcular $\displaystyle \lim_{x\rightarrow 0}\,(f(x)-\dfrac{2}{g(x)})$
b) Calcular la ecuación de la recta tangente a la curva $y=f(x)$ en el punto $(\dfrac{1}{2}\,,\,4)$
c) Calcular el área delimitada por la curva $y=f(x)$ y la recta $y=-x+3$
SOLUCIÓN.
a)
Cuando $x \rightarrow 0$, $x \sim \sin\,x$ ( son infinitésimos equivalentes ), luego $$\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{\sin\,x})=2\,\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{x})=0$$
b)En $x=\dfrac{1}{2}$ podemos determinar la recta tangente a la gráfica de la función $f(x)$ pues en ese punto la función es derivable. Sea la ecuación en forma explícita de la recta tangente $t:y=mx+k$ en dicho punto. Vamos a determinar los valores de los coeficientes $m$ ( pendiente de la recta ) y $k$ ( ordenada en el origen ).
$m\overset{\text{def}}{=}f'(1/2)=((\dfrac{2}{x})')|_{x=1/2}=(-\dfrac{2}{x^2})|_{x=1/2}=-8$, con lo cual podemos escribir $t:y=-8\,x+k$, veamos ahora, cuál es el valor de $k$: como en $x=1/2$ se tiene que cumplir que $f(1/2)=(-8\,x+k)_{x=1/2}$, vemos que $f(1/2)=-8\cdot \dfrac{1}{2} +k$, luego $k=f(1/2)+4$, esto es, $k=(\dfrac{2}{1/2})+4=8$. Así concluimos que la ecuación de la recta tangente pedida es $t:y=-8\,x+8$
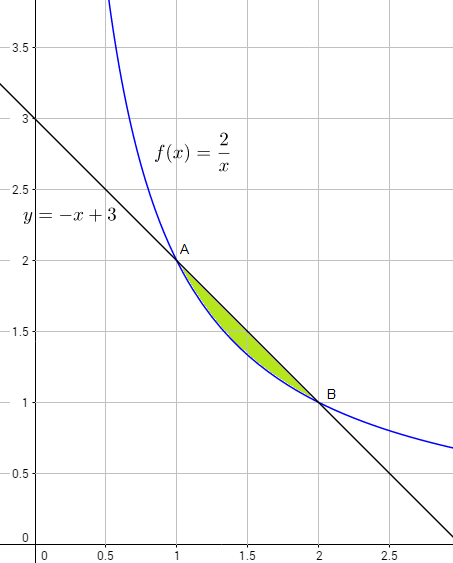
c) El siguiente gráfico ( las gráficas de las dos funciones inciden en el primer cuadrante ) ayuda a visualizar el área pedida
Entonces, $$\text{Área}=\displaystyle \int_{x_A}^{x_B}\,((-x+3)-f(x))\,dx=\int_{x_A}^{x_B}\,((-x+3)-\dfrac{2}{x})\,dx \quad \quad (1)$$ Necesitamos conocer los límite de integración, que son las abscisas de los puntos de intersección $A$ y $B$, y que se calculan resolviendo la ecuación $$\dfrac{2}{x}=-x+3$$ esto es $$x^2-3x+2=0\Leftrightarrow x=\dfrac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2 \cdot 1}=\dfrac{3\pm 1}{2}=\left\{\begin{matrix}2 \\ 1 \end{matrix}\right.$$ con lo cual $x_A=1$ y $x_B=2$
Así, de (1), $$\text{Área}=\displaystyle \int_{1}^{2}\,\dfrac{-x^2+3x-2}{x}\,dx=\int_{1}^{2}\,(-x+3-\dfrac{2}{x})\,dx=\displaystyle -\dfrac{1}{2}\,\left[x^2\right]_{1}^{2}+3\,\left[x\right]_{1}^{2}-2\,\left[\ln\,x\right]_{1}^{2}$$
$=-\dfrac{1}{2}\cdot (4-1)+3\cdot (2-1)-2\cdot (\ln\,2-\ln\,1)=-\dfrac{3}{2}+3-2\,\ln\,2=$
$=(\dfrac{3}{2}-2\,\ln\,2) \; \text{u.a.} \approx 0,1137 \; \text{u.a.}$
$\square$
a) Calcular $\displaystyle \lim_{x\rightarrow 0}\,(f(x)-\dfrac{2}{g(x)})$
b) Calcular la ecuación de la recta tangente a la curva $y=f(x)$ en el punto $(\dfrac{1}{2}\,,\,4)$
c) Calcular el área delimitada por la curva $y=f(x)$ y la recta $y=-x+3$
SOLUCIÓN.
a)
Cuando $x \rightarrow 0$, $x \sim \sin\,x$ ( son infinitésimos equivalentes ), luego $$\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{\sin\,x})=2\,\displaystyle \lim_{x\rightarrow 0}\,(\dfrac{2}{x}-\dfrac{2}{x})=0$$
b)En $x=\dfrac{1}{2}$ podemos determinar la recta tangente a la gráfica de la función $f(x)$ pues en ese punto la función es derivable. Sea la ecuación en forma explícita de la recta tangente $t:y=mx+k$ en dicho punto. Vamos a determinar los valores de los coeficientes $m$ ( pendiente de la recta ) y $k$ ( ordenada en el origen ).
$m\overset{\text{def}}{=}f'(1/2)=((\dfrac{2}{x})')|_{x=1/2}=(-\dfrac{2}{x^2})|_{x=1/2}=-8$, con lo cual podemos escribir $t:y=-8\,x+k$, veamos ahora, cuál es el valor de $k$: como en $x=1/2$ se tiene que cumplir que $f(1/2)=(-8\,x+k)_{x=1/2}$, vemos que $f(1/2)=-8\cdot \dfrac{1}{2} +k$, luego $k=f(1/2)+4$, esto es, $k=(\dfrac{2}{1/2})+4=8$. Así concluimos que la ecuación de la recta tangente pedida es $t:y=-8\,x+8$
c) El siguiente gráfico ( las gráficas de las dos funciones inciden en el primer cuadrante ) ayuda a visualizar el área pedida
Entonces, $$\text{Área}=\displaystyle \int_{x_A}^{x_B}\,((-x+3)-f(x))\,dx=\int_{x_A}^{x_B}\,((-x+3)-\dfrac{2}{x})\,dx \quad \quad (1)$$ Necesitamos conocer los límite de integración, que son las abscisas de los puntos de intersección $A$ y $B$, y que se calculan resolviendo la ecuación $$\dfrac{2}{x}=-x+3$$ esto es $$x^2-3x+2=0\Leftrightarrow x=\dfrac{-(-3)\pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2 \cdot 1}=\dfrac{3\pm 1}{2}=\left\{\begin{matrix}2 \\ 1 \end{matrix}\right.$$ con lo cual $x_A=1$ y $x_B=2$
Así, de (1), $$\text{Área}=\displaystyle \int_{1}^{2}\,\dfrac{-x^2+3x-2}{x}\,dx=\int_{1}^{2}\,(-x+3-\dfrac{2}{x})\,dx=\displaystyle -\dfrac{1}{2}\,\left[x^2\right]_{1}^{2}+3\,\left[x\right]_{1}^{2}-2\,\left[\ln\,x\right]_{1}^{2}$$
$=-\dfrac{1}{2}\cdot (4-1)+3\cdot (2-1)-2\cdot (\ln\,2-\ln\,1)=-\dfrac{3}{2}+3-2\,\ln\,2=$
$=(\dfrac{3}{2}-2\,\ln\,2) \; \text{u.a.} \approx 0,1137 \; \text{u.a.}$
$\square$
Etiquetas:
análisis de funciones,
área de un recinto,
integral definida
Suscribirse a:
Entradas (Atom)