Analizar la continuidad y la derivabilidad de la función en ... ( Artículo escrito en catalán )

Enunciat:
Considereu la següent funció:
$f(x)=\left\{\begin{matrix}(x+1)^3 \quad \text{si} \quad x \le 0\\\\2 \quad \text{si} \quad x=1\\\\-x^2+2 \quad \text{si} \quad x > 0 \; \wedge \; x \neq 1\\ \end{matrix}\right.$

Us demanem:

    a) La representació gràfica de la funció

    b) Localitzeu els punts de discontinuïtat i classifiqueu-los de forma analítica. Digueu de quin tipus de discontinuïtat es tracta. [ Cal que raoneu a partir dels valors dels límits laterals (si existeixen), del límit global (si existeix o no), i del valor de la funció en el punt de discontinuïtat considerat ( si la funció està definida en aquest punt, és clar )]

    c) Calculeu el valor de la derivada de la funció per al punt d'abscissa $x=-1$

    d) Indiqueu per a quins valors de la variable independent la funció no és derivable. Expliqueu per què.

Resolució:
a)   Dibuixem el gràfic (vegeu la Figura 1) d'acord amb la definició (a troços) de la funció; a partir del traç de la paràbola semicúbica $x^3$ (desplaçada una unitat en el sentit negatiu de l'eix d'abscisses), i dibuixant el traç de la funció quadràtica $x^2$ (desplaçada dues nunitats en el sentit positiu de l'eix d'ordenades i invertint-la).
$\square$

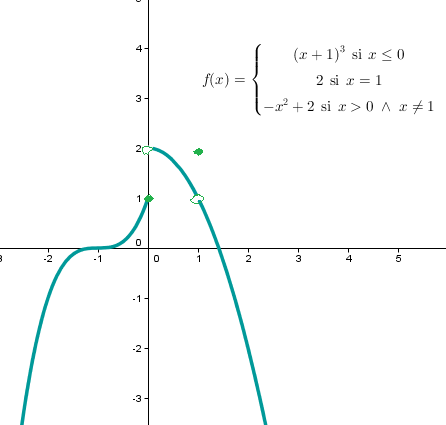
Figura 1

b)   La funció presenta una discontinuïtat essencial de primera espècie (en concret, de salt finit) per a $x=0$, atès que el els límits laterals existeixen i tenen valor finit, però no coincideixen
$\displaystyle \lim_{x \rightarrow 0^{+}}\,f(x)=1$
i
$\displaystyle \lim_{x \rightarrow 0^{-}}\,f(x)=2$
per aquesta raó
$\displaystyle \nexists \lim_{x \rightarrow 0}\,f(x)$

Per altra banda, hi ha una discontinuïtat no essencial (evitable) a $x=1$ perquè per bé que
$\displaystyle \exists \lim_{x \rightarrow 1}\,f(x)$ (i és igual a $1$), el seu valor no és igual al valor de la funció per a $x=1$ (que és igual a $2$)
$\square$

c)   Per a calcular $f^{'}(-1)$, tindrem en compte que [ d'acord amb la definició de la funció ], per a $x=-1$, cal derivar l'expressió del primer tram, que és igual a
$\bigg( (x+1)^3 \bigg)^{'}=3\,(x+1)^2$
Per a $x=-1$ pren el valor
$3\,(-1+1)^2=0$
$\square$

d)   Lògicament, la funció no és derivable en els punts on és discontínua: $x=0$ i $x=-1$. Per altra banda, per a la resta de punts del domini d'existència ( $D = \mathbb{R}$ ), el límit que defineix la derivada existeix (els límits laterals existeixen i coincideixen) i, per tant, la funció és derivable en tots aquests altres punts.
$\square$

[nota del autor]