Cálculo de una integral definida (un ejemplo). Aplicación de la regla de Barrow

Para calcular, a modo de ejemplo, la integral definida $$\displaystyle \int_a^b\,3^x\,dx\,,\,\text{donde}\,a\lt b$$ necesitamos calcular, en primer lugar, la integral indefinida $$\displaystyle \int\,3^x\,dx$$ esto es, la familida de funciones primitivas $F(x)+C$ (siendo $C$ la constante arbitraria de integración), tales que, por el primer teorema del cálculo integral, cumpla que $\dfrac{d(F(x)+C)}{dx}=f(x)$, siendo $f(x)$ la función del integrando, es decir, $f(x)=3^x$

Veamos, primero, cuál es esa familia de funciones primitivas: $\displaystyle \int\,3^x\,dx\overset{[3=e^{\ln\,3}]}{=} \int\,\left(e^{\ln\,3}\right)^x\,dx=\int\,e^{x\,(\ln\,3)}\,dx \overset{(1)}{=}\int\,e^{x\,(\ln\,3)}\,\dfrac{d(x\,(\ln\,3))}{\ln\,3}=\dfrac{e^{x\,(\ln\,3)}}{\ln\,3} =\dfrac{3^x}{\ln\,3}+C$. Entonces, por el segundo teorema fundamental del cálculo integral (regla de Barrow), y a partir de cualquier función primitiva, por ejemplo $F(x)=\dfrac{3^x}{\ln\,3}$ (tomando, por ejemplo, $C=0$) tenemos que $\displaystyle \int_a^b\,3^x\,dx\overset{(2)}{=}F(b)-F(a)=\dfrac{3^b}{\ln\,3}-\dfrac{3^a}{\ln\,3}=\dfrac{1}{\ln\,3}\left(3^b-3^a\right)$

-oOo-

Nota (1):
Este paso, en realidad, es un cambio de variable: $u:=x\,(\ln\,3)$ y por tanto $du=\left( x\,(\ln\,3) \right)'\,dx = (\ln\,3)\cdot 1\,dx = (\ln\,3)\,dx \Rightarrow dx=\dfrac{du}{\ln\,3}$, con lo cual $\displaystyle \int\,e^{x\,(\ln\,3)}\,dx = \int\,e^u\,\dfrac{du}{\ln\,3}=\dfrac{1}{\ln\,3}\,e^u+C=\dfrac{1}{\ln\,3}\,e^{(\ln\,3)\,x}+C=\dfrac{3^x}{\ln\,3}+C$

Nota (2):
Otra manera de notar la aplicación de la regla de Barrow es: $\displaystyle \displaystyle \int_a^b\,3^x\,dx=\left[ \dfrac{3^x}{\ln\,3} \right]_{a}^{b}=\dfrac{3^b}{\ln\,3}-\dfrac{3^a}{\ln\,3}=\dfrac{1}{\ln\,3}\left(3^b-3^a\right)$

Nota (3):
Podemos aplicar también la regla de Barrow a partir del cambio de variable (véase (1)) realizado y recalculando los nuevos límites de integración: $\displaystyle \int_{a}^{b}\,3^x\,dx=\int_{a}^{b}\,e^{x\,(\ln\,3)}\,dx\overset{(1)}{=}\int_{a\,\ln\,3}^{b\,\ln\,3}\,e^u\,\dfrac{du}{\ln\,3}=\left( \dfrac{e^{b\,\ln\,3}}{\ln\,3}-\dfrac{e^{a\,\ln\,3}}{\ln\,3}\right)=\dfrac{1}{\ln\,3}\,\left( e^{b\,\ln\,3} - e^{a\,\ln\,3}\right)=\dfrac{1}{\ln\,3}\,\left( 3^b-3^a \right)$

$\diamond$

Para personas interesadas en la preparación de las Olimpiadas Matemáticas (entre otros intereses): una aplicación práctica de la función especial $W$ de Lambert a la resolución de ecuaciones trascendentes de los tipos $x^x=a$, $x\,b^x=c$ y $a^{k\,x}=f(x)$, donde $a,b,c,k\in \mathbb{R}$ y $f(x)$ es una función lineal afín, en el cuerpo de los números reales

En este artículo voy a explicaros cómo podemos calcular la solución de una ecuación trascendente del tipo referido en el título. Voy a empezar resolviendo un caso sencillo, tal como $x^x=a$ para $x\in \mathbb{R}$ y siendo $a$ una constante a la cual le asignaremos el valor $2$, para dar consistencia práctica a este ejemplo. Después, resolveré casos un poco más complicados. Utilizaremos la función $W$ de Lambert, aunque en los tiempos que corren esto no esté incluído en el curriculo oficial de esta asignatura; sin embargo, sí se enseña este procedimiento a las personas interesadas en los problemas del tipo Olimpiada Matemática. Creo que aprender a hacerlo es muy útil, pues representa una vía de resolución alternativa a los métodos numéricos tales como el método de bisección (que sí se estudian en esta asignatura).

La función especial $W$ de Lambert se define de la siguiente manera: la función inversa (recíproca) de la función $f(x)=x\,e^x$ es $f^{-1}(x):=W(x)$, o lo que es lo mismo, si $y=x\,e^x$, se tiene que $W(y)=x$; dicho de otra forma: $W(x\,e^x)=x$ \quad (1), lo cual, también, lleva a poder escribir que $W(x)\,e^{W(x)}=x$ (siendo, en general, $x \in \mathbb{C}$). Dicha función tiene varias ramas, y sus valores pueden calcularse mediante algoritmos de cálculo numérico, que, al final, deberemos utilizar la mayor parte de las veces que necesitemos emplear dicho recurso. Suelo recurrir a la utilidad en línea WolframAlpha para esta finalidad.

Esa función especial de Lambert es de la que nos valdremos para resolver una ecuación de este tipo, eso sí, para no complicarnos excesivamente, nos restringiremos a operar con números reales.

Dicha función presenta varias ramas, para un mismo valor $k\in \mathbb{R}$, que se suelen designar mediante un subíndice: $W_{-1}(k), W_{0}(k), W_{1}(k),\ldots$, de las cuales en este caso en el que buscamos una solución en $\mathbb{R}$, solamente nos interesa la rama $W_{0}(k)$, cuyo valor (para un valor concreto de $k \in \mathbb{R}$ dado) podemos conocer consultando las tablas apropiadas o incluso consultar en línea alguna aplicación matemática, como por ejemplo Wolframalpha [https://www.wolframalpha.com/].

Desde luego, ni que decir tiene que, conocer a fondo la función $W$ de Lambert requiere un estudio exhaustivo y huelga decir que tal cosa sí corresponde a un curso universitario; pero, a efectos prácticos, lo que he dicho arriba es suficiente para resolver con elegancia este tipo de ecuaciones «sencillas» para un nivel de matemáticas de bachillerato, a partir, únicamente de la comprensión de la utilidad práctica de la propiedad (1).

Ejemplo 1

Bien, pues, el ejercicio de muestra que voy a tratar es (como ya he comentado) la resolución de la ecuación $x^x=2$, donde $x\in \mathbb{R}$. Lo describo a continuación, con algunos pasos algebraicos necesarios, paso a paso:
  $x^x=2$
    $\ln\,(x^x)=\ln\,2$
      $x\,\ln\,x=\ln\,2$
        $(e^{\ln\,x})\,\ln\left(e^{\ln\,x}\right)=\ln\,2$
          $(e^{\ln\,x})\,(\ln\,x)\,( \ln\,e)=\ln\,2$
            $(e^{\ln\,x})\,(\ln\,x)\cdot 1=\ln\,2$
              $(\ln\,x)\,e^{\ln\,x}=\ln\,2$
                $W\left((\ln\,x)\,e^{\ln\,x}\right)=W(\ln\,2)$
                  $W\left((\ln\,x)\,e^{\ln\,x}\right)=W(\ln\,2)$
                    $\ln\,x \overset{(1)}{=}W(\ln\,2)$, siendo el argumento de $W$, ahora, en particular, perteneciente a $\mathbb{R}$
                      $x=e^{W_{0}(\ln\,2)}=\;$ [Wolframalpha] $\;{\approx}1,5596 $.

-oOo-

Comprobación:

Sustituyamos el valor encontrado en la ecuación original y veamos si se cumple la igualdad numérica entre ambos miembros:
  $1,5596^{1,5596}\overset{?}{=}2$
    $1,5596^{1,5596}\overset{\text{calculadora científica}}{=}1.99997...\approx 2$, que es (prácticamente) igual a la cantidad del segundo miembro.

Algunos ejemplos más:

Ejemplo 2

Voy a resolver ahora una ecuación algo distinta, tal como $2^x=\dfrac{1}{x}$. Para ello, como siempre, y en primer lugar, tendremos que trabajar un poco con el álgebra elemental para escribir la ecuación de tal manera que la aplicación de la propiedad reseñada arriba pueda utilizarse de manera bien clara:

$2^x=\dfrac{1}{x}$
  $x\,2^x=1 \quad (1)$
    $x\,\left(e^{\ln\,2}\right)^x=1$, habida cuenta de que $2\equiv e^{\ln\,2}$
      $x\,e^{x\,\ln\,2}=1$
        $(x\,\ln\,2)\,e^{x\,\ln\,2}=1\cdot \ln\,2$
          $W\left((x\,\ln\,2)\,e^{x\,\ln\,2}\right)=W(\ln\,2)$
            $x\,\ln\,2=W(\ln\,2)$
              $x=\dfrac{W(\ln\,2)}{\ln\,2}$
Consultando el valor de la función de Lambert para $\ln\,2$, vemos que $W(\ln\,2)\approx 0,4444$, lo cual lo he hecho mediante el asistente en línea WolframAlpha:

  W_0(log(2))
  Aproximación decimal
  0, 4444360910188604811868963306448808771676930202799304144725290184...

Por tanto, una aproximación del resultado exacto es $\dfrac{W(\ln\,2)}{\ln\,2}\approx 0,6411$

Comentario:
Dibujando las gráficas que corresponden a la función del miembro izquierdo, $f(x)=x\,2^x$, y derecho, $g(x)=1$ de $(1)$ se ve claramente que se intersecan en un sólo punto; así pues, la abscisa del mismo corresponde a la solución exacta encontrada.

Comprobación:

Sustituyendo este valor en la ecuación original: $2^{0,6411} \overset{?}{=} \dfrac{1}{0,6411}$. Vemos que el resultado aproximado puede darse por satisfactorio, pues el valor del primer miembro de la igualdad aproximada es $1,5595$, y el del segundo miembro es igual a $1,5598$, que difieren en tres diezmilésimas.

Ejemplo 3

Resolveré ahora una ecuación parecida: $2^x=2\,x$
que puedo escribirla de la forma,
  $2\,x\,2^{-x}=1$
    $2\,x\,\left(e^{\ln\,2}\right)^{-x}=1$
      $2\,x\,e^{-x\,\ln\,2}=1$
        $x\,e^{-x\,\ln\,2}=\dfrac{1}{2}$
          $-x\,e^{-x\,\ln\,2}=-\dfrac{1}{2}$
            $(-(\ln\,2)\,x)\,e^{-x\,\ln\,2}=-\dfrac{\ln\,2}{2}$
              $W\left(-(\ln\,2)\,x)\,e^{-x\,\ln\,2}\right)=W\left(-\dfrac{\ln\,2}{2}\right)$
              $-(\ln\,2)\,x=W\left(-\dfrac{\ln\,2}{2}\right)$
                $x=-\dfrac{W\left(-\dfrac{\ln\,2}{2}\right)}{\ln\,2}$
Consultando ahora el valor de la función W de Lambert con, por ejemplo, la ayuda de WolframAlpha:

obtenemos el resulado:
                $x=1$, cuya comprobación es inmediata.

Ejemplo 4

Otro caso interesante es, por ejemplo, el de la ecuación $2^x=x+1$, en la que he añadido un término constante al segundo miembro. También se ve claramente cuáles son los valores de la solución a simple vista: tanto $0$ como $1$ satisfacen la igualdad; en efecto, $2^0=1=0+1=1$ y $2^1=2=1+1=2$. Como en el ejemplo anterior, y aún a sabiendas de lo que debo encontrar, voy a seguir aplicando la técnica de la función de Lambert, lo cual será un agradable ejercicio, pues podremos comprobar si todo encaja. Empecemos pues con el juego algebraico apropiado para ir dando forma apropiada al argumento de la función W de Lambert. Démonos cuenta de que, en el fondo, en todos los casos expuestos estoy haciendo esencialmente lo mismo, esto es, reexpresar lo necesario de manera equivalente para poder utilizar esa interesante propiedad de la función especial de Lambert. Empecemos:
  $2^x=x+1$
    $(x+1)\,2^{-x}=1$
      $(x+1)\,2^{-x-1}\,2^1=1$
        $(x+1)\,2^{-x-1}=\dfrac{1}{2}$
          $-(x+1)\,2^{-(x+1)}=-\dfrac{1}{2}$
            $-(x+1)\,(e^{\ln\,2})^{(-(x+1))}=-\dfrac{1}{2}$
              $-(x+1)\,e^{-((\ln\,2)\,(x+1))}=-\dfrac{1}{2}$
                $(-(\ln\,2)\,(x+1))\,e^{(-(\ln\,2)\,(x+1))}=-\dfrac{1}{2}\,\ln\,2$
                  $W\left((-(\ln\,2)\,(x+1))\,e^{(-(\ln\,2)\,(x+1))}\right)=W(-\dfrac{\ln\,2}{2})$
                    $-(\ln\,2)\,(x+1)=W(-\dfrac{\ln\,2}{2})$
                      $x+1=-\dfrac{W(-\dfrac{\ln\,2}{2})}{\ln\,2}$
                        $x=-\dfrac{W(-\dfrac{\ln\,2}{2})}{\ln\,2}-1=1-1=0$
Obsérvese que si bien llegamos a uno de los dos valores que habíamos encontrado de un vistazo, $x_1=0$, no llegamos, en principio, a encontrar el segundo: $x_2=1$. Ello es debido a que la función de Lambert tiene más enjundia de lo que, sin querer, he llevado a hacer creer, pues, en realidad, tiene varias ramas, las cuales se designan por $W_n$ con $n\in \mathbb{Z}$.
Fijémonos en lo que nos da WolframAlpha como resultado general:

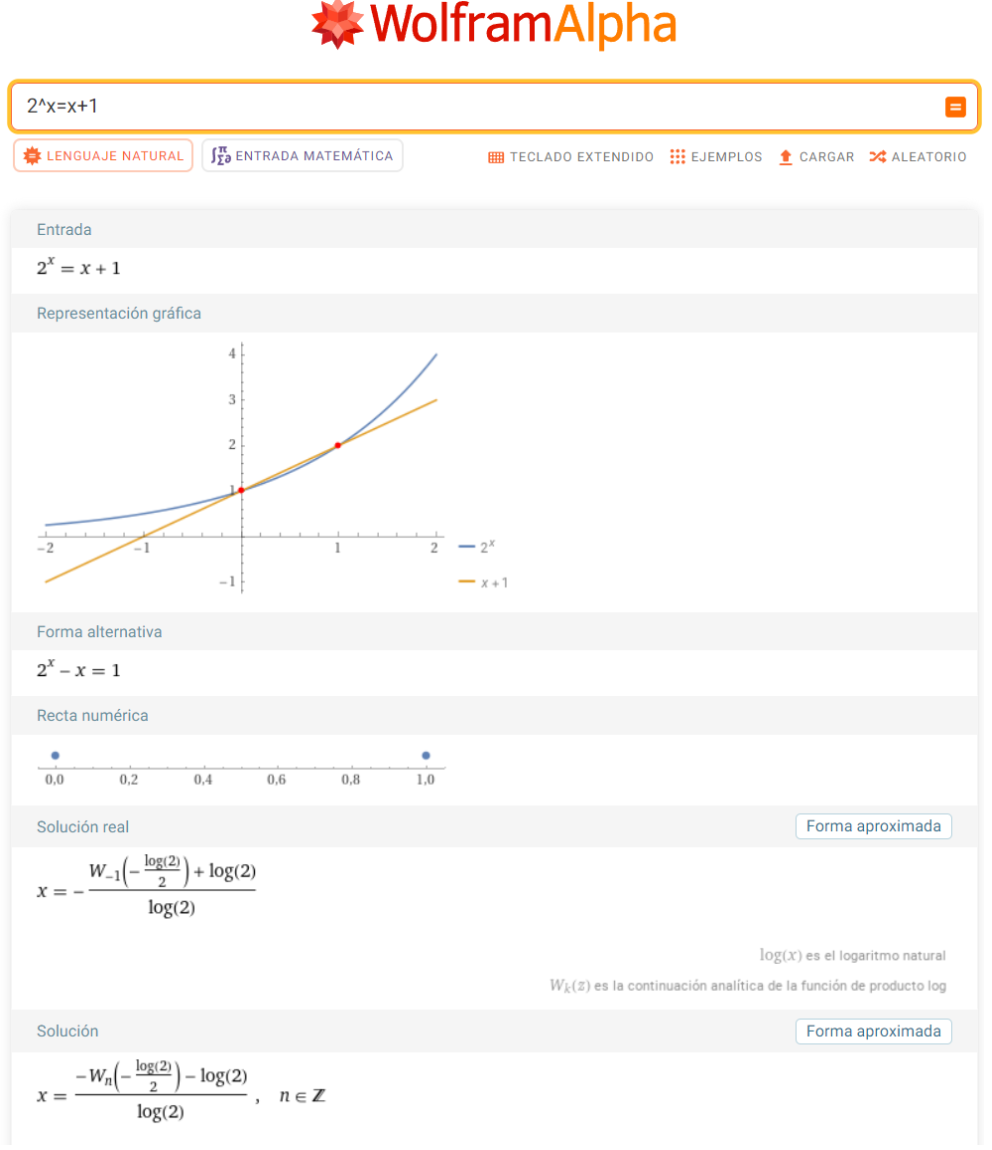
La ausencia en lo encontrado del segundo valor tiene que ver con el hecho de que sólo estoy utilizando una de las ramas múltiples ramas. Dicho ésto, no voy a profundizar más, siendo consciente que debo ceñirme a las posibilidades de comprensión para un nivel de segundo de Bachillerato. En cualquier caso, a las personas que estén muy interesadas, les sugiero la lectura de ampliación de la referencia [1], cuyo autor es el profesor Ángel Franco García, y en el que hace un estudio para $W_{-1}$ y $W_{0}$.

Ejemplo 5

Estudiemos ahora esta otra ecuación $2^x=2x+6$, que es similar a la anterior, y como se aprecia en la gráfica, la intersección de una función lineal afín con una función exponencial, da lugar a dos puntos; sus abscisas representan los valores que forman la solución de la ecuación.

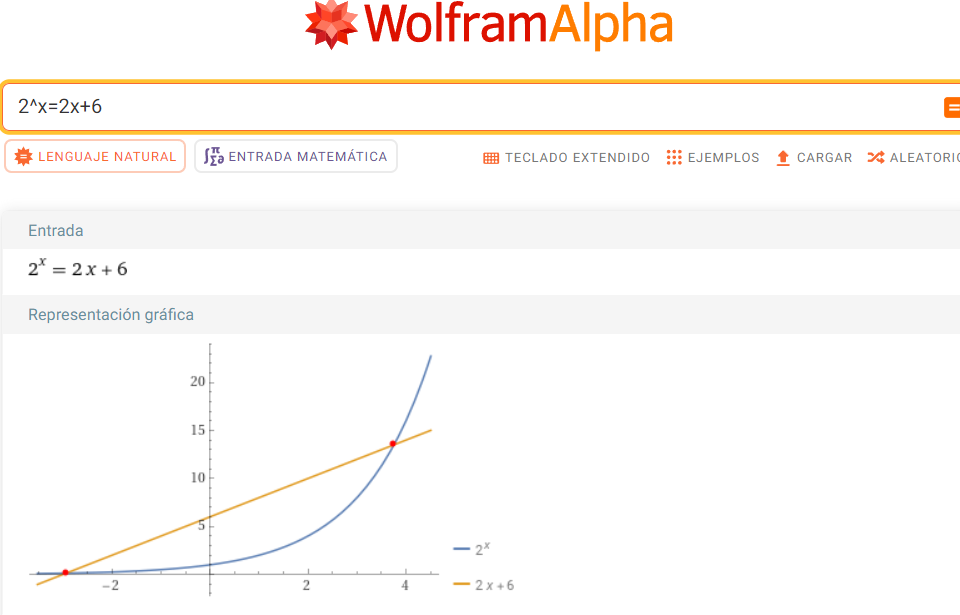
Sigamos aplicando la técnica basada en la función W de Lambert para ver qué encontramos de esa manera:
  $2^x=2x+6$
    $2^x=2\,(x+3)$
      $2\,(x+3)\,2^{-x}=1$
        $2\cdot \,2^3\,(x+3)\,2^{-x-3}=1$
          $2^4\,(x+3)\,2^{-x-3}=1$
            $(x+3)\,2^{-x-3}=2^{-4}$
              $(x+3)\,(e^{\ln\,2})^{-x-3}=2^{-4}$
                $(x+3)\,e^{(-x-3)\,\ln\,2)}=2^{-4}$
                  $((-\ln\,2)(x+3))\,e^{(-(\ln\,2)\,(x+3)))}=(-\ln\,2)\cdot 2^{-4}$
                    $W\left(((-\ln\,2)(x+3))\,e^{(-(\ln\,2)\,(x+3)))}\right)=W\left((-\ln\,2)\cdot 2^{-4}\right)$
                      $(-\ln\,2)(x+3)=W\left((-\ln\,2)\cdot 2^{-4}\right)$
                        $x+3=\dfrac{W\left((-\ln\,2)\cdot 2^{-4}\right)}{-\ln\,2}$
                          $x=-\dfrac{W\left((-\ln\,2)\cdot 2^{-4}\right)}{\ln\,2}-3$
                            $x=-\dfrac{W\left(\frac{-\ln\,2}{16}\right)}{\ln\,2}-3$
Consultando (véase la figura abajo) el valor de la función de Lambert para el argumento dado, vemos que $W\left(\frac{-\ln\,2}{16}\right)\approx -0,0453$

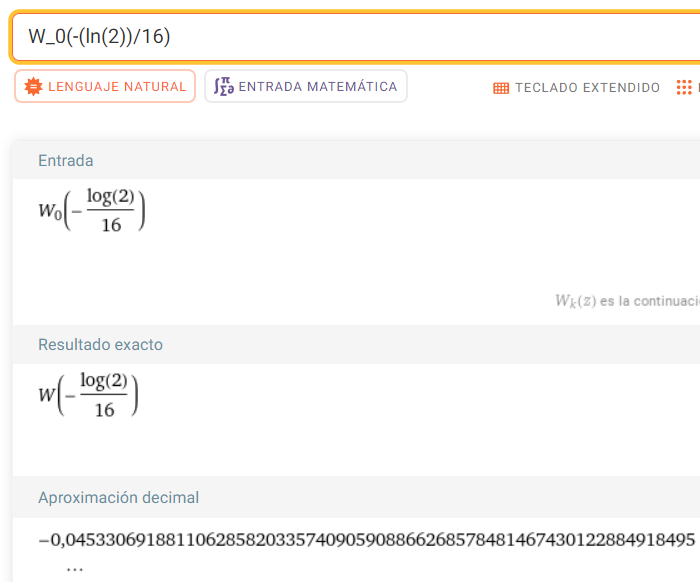
Por tanto, el resultado aproximado del valor que se deduce en la línea de arriba es $x\approx -\dfrac{-0,0453}{\ln\,2}-3=-2,9346$. ¿Y qué ocurre con el segundo valor que deberíamos encontrar (próximo a $4$)? Pues bien, cabe aquí hacer el mismo comentario que en el ejemplo anterior, por lo que se refiere a las ramas de $W$ que no hemos utilizado; así que, de momento, no profundizaremos más. -oOo-

Referencias para el profesor:

  [1]   [http://www.sc.ehu.es/sbweb/fisica3/especial/lambert/lambert.html]
  [2]   [https://es.wikipedia.org/wiki/Función_especial]
  [3]   [WolframAlpha]

$\diamond$

Un recurso de cálculo de 'cajón de sastre' para realizar algunos cálculos aproximados

Un recurso bastante útil en algunas situaciones en las que la base de una función exponencial no es el número $e$ se basa en la siguiente propiedad, que es válida para $\mathbb{R} \ni a\gt 0$: $$a=e^{\ln\,a}$$ En efecto, sacando logaritmos en base $e$ en cada miembro, $$\ln\,a=\ln\,\left(e^{\ln\,a}\right)=(\ln\,a)\cdot \ln\,e=(\ln\,a)\cdot 1=\ln\,a$$

Así, por ejemplo, para derivar la función $f(x)=a^x$, donde $a\neq e$, la podemos, en primer lugar, reescribir de la forma $f(x)=a^x=\left(e^{\ln\,a}\right)^x=e^{ex\,\ln\,a}$ y, a continuación, aplicar la regla de derivación de la función exponencial de base $e$, además de la regla de la cadena: $$f'(x)=\left(a^x\right)'=\left(\left(e^{\ln\,a}\right)^x\right)'=\left(e^{(\ln\,a)\,x}\right)'=(\ln\,a)\,e^x$$

Otra interesante utilidad que nos brinda este recurso es el de hacer algunos cálculos aproximados de una manera bastante eficaz, sobre todo si no disponemos de recursos suficientes. Pongamos que deseamos calcular el resultado aproximado de $\sqrt[10]{3}$, y que la única herramienta de que disponemos es un libro de tabls de logaritmos; pues bien, primero, reescribamos convenientemente nuestro problema: $$\sqrt[10]{3}=3^{\frac{1}{10}}=\left(e^{\ln\,3}\right)^\frac{1}{10}$$ Consultando ahora nuestras tablas de logaritmos, vemos que el valor de $\ln\,3$ con una precisión de hasta la cuerta cifra decimal es $1,0986$, con lo cual $\sqrt[10]{3}=\left(e^{1,0986}\right)^{\frac{1}{10}}=e^{0,10986}$

Finalmente, tengamos en cuenta que, en las proximidades de $x=0$, la función $f(x)=e^x$ es muy parecida a la función $g(x)=1+x$ (basta con desarrollar en serie de Tylor la función $f(x)$ alrededor de $x=0$ y truncarla en el segundo término (de orden $1$), y como, en ese sentido, $0,10986$ es un número razonablemente pequeño (cercano a $0$), podemos hacer la siguiente aproximación $e^{0,10986} \approx 1 + 0,10986 = 1,10986$ de la cual tomaremos, siendo conservadores en nuestra pretensiones, tres cifras significativas, esto es, $e^{0,10986} \approx 1,11$, pudiendose comprobar que las tres son cifras significativas correctas. $\diamond$